Углы между прямыми и плоскостями

Углом между двумя скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными двум данным скрещивающимся прямым

Углом между плоскостью и прямой (непараллельной и неперпендикулярной данной плоскости) называется острый угол между прямой и ее проекцией на данную плоскость

Теорема: угол между прямой и плоскостью есть наименьший из углов, которые эта прямая образует со всеми прямыми, лежащими в этой плоскости.

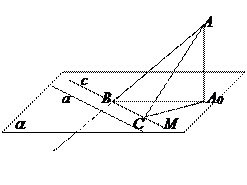Доказательство: Пусть дана прямая АВ которая пересекает плоскость a в точке В, АВ 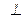a. Пусть а – произвольная прямая, лежащая в плоскости a. Возьмем точку А на прямой АВ и опустим из нее перпендикуляр на плоскость a, получим проекцию точки А – А₀. Угол между прямой и плоскостью - ÐАВА₀. Проведем ВМ//а. Угол между прямой АВ и прямой а равен углу ÐАВМ. Покажем, что ÐАВМ>ÐАВА₀. Для этого построим точку С 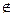ВМ такую, что ВС=ВА₀. Соединим АС и рассмотрим треугольники DВАА₀ и DВСА. У них АВ – общая, ВА₀=ВС, но АС>АА₀, т.к. любая наклонная больше перпендикуляра, проведенного из той же точки. Следовательно ÐАВС>ÐАВА₀, т.к. против большей стороны лежит больший угол.

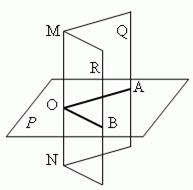Двугранным углом называется фигура, образованная двумя полуплоскостями, ограниченными общей прямой. Эта прямая называется ребром двугранного угла, а две полуплоскости – его гранями. Обозначается: ÐQMNR

Линейным углом двугранного угла называется уголÐАОВ, образованный перпендикулярами, проведенными к ребру двугранного угла в обеих гранях через одну и ту же точку ребра.

Двугранный угол измеряется своим линейным углом.

Два двугранных угла называются равными, если один из них можно наложить на другой таким образом, чтобы они совпали.

Два двугранных угла называются прилежащими, если они имеют общее ребро и общую грань и расположены по разные стороны от этой общей грани.

Перпендикулярность прямых и плоскостей.

Прямая называется перпендикулярной к плоскости, если она перпендикулярна ко всем прямым лежащим в этой плоскости.

Теорема: Прямая перпендикулярная к каким-либо двум пересекающимся прямым, лежащим в некоторой плоскости, перпендикулярна к этой плоскости.

Доказательство: самостоятельно

Теорема: Две прямые, перпендикулярные к одной плоскости параллельны.

Доказательство:

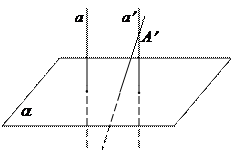
Пусть дана плоскость α и прямые а и а¢^ α.

Докажем, что а // а¢. Построим а¢¢, такую, что а¢¢// а и а¢¢ проходит через точку А¢ Î а¢. Так как а ^ α, то и а¢¢ ^ α (почему?

). Тогда из одной точки опущены два перпендикуляра. Следовательно, они совпадают. Значит, а¢ // а.

Теорема: Прямая, не перпендикулярная плоскости перпендикулярна бесчисленному множеству прямых, лежащих в этой плоскости, а именно перпендикулярна ко всем прямым, перпендикулярным к проекции данной прямой на данную плоскость и только к этим прямым.

Доказательство:

Возможны два случая:

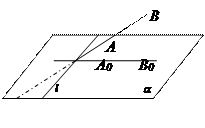
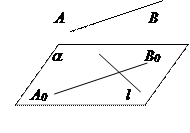
1) АВÇa¹Æ 2) АВ//a

Докажем первую часть.

1. Пусть А₀В₀ – проекция АВ на α. Прямая l Î α, l ^ А₀В₀. Докажем, что l ^ АВ.

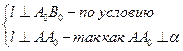Þ l ^ плоскости АА₀В₀ Þ l ^ АВ.

2. Пусть АВ ^ l, l Î α.

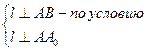Þ l ^ АА₀В Þ l ^ А₀В₀.

.

Следствие 1 (теорема о трех перпендикулярах).Прямая, лежащая в некоторой плоскости проходит через основание данной наклонной и перпендикулярна к самой наклонной.

Доказательство: самостоятельно.

Следствие 2: Прямая, лежащая в некоторой плоскости проходит через основание наклонной и к ней перпендикулярная, перпендикулярна и к проекции наклонной.

Доказательство: самостоятельно.

Плоскость называется перпендикулярной к другой плоскости, если она образует с этой

плоскостью равные между собой прилежащие двугранные углы.

Двугранный угол называется прямым, если одна из его граней перпендикулярна к другой.

Теорема: Если две плоскости перпендикулярны, то любой перпендикуляр к линии их пересечения лежащий в одной из плоскостей является перпендикуляром к другой плоскости.

Доказательство:

Ð N×XY×P – двугранный (прямой).

Пусть α ^ b. АО ^ ХУ, АО Î b.

Докажем, что АО ^ α.

АО – сторона линейного угла. Проведем ОВ ^ ХУ – другую сторону этого линейного угла. Так как α ^ b, то ÐАОВ = 90°, и из того, что

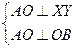Þ АО ^ α.

Теорема: Плоскость перпендикулярна к другой плоскости, если она проходит через перпендикуляр к последней.

Доказательство: Пусть АО ^ α и АО Î b. Из того, что АО ^ α следует, что ОА перпендикулярна любой прямой Î α:

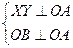
Где ОВ ^ ХУ. Тогда ÐАОВ – линейный угол двугранного угла Ð N×XY×P – ÐАОВ = 90° Þ двугранный угол Ð N×XY×P =90°. Значит плоскости α и b перпендикулярны. .

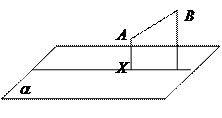
Теорема: Через прямую, не перпендикулярную плоскости проходит плоскость, перпендикулярная данной и притом только одна.

Доказательство:

1. Пусть АВ не перпендикулярна α. Причем она может лежать в плоскости или быть вне ее. Проведем АХ ^ α. Тогда плоскость ХАВ ^ α.

2. Любая плоскость p, проведенная через АВ перпендикулярно к α проходит через прямую АХ, так как перпендикуляр, спущенный на α из точки А будет совпадать с перпендикуляром, проведенным из А на линию пересечения плоскостей, Þ плоскость p совпадает с плоскостью ХАВ.

Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из данной точки на плоскость.

Теорема: Если даны две скрещивающиеся прямые, то существует прямая и притом только одна, которая пересекает обе прямые под прямым углом. Эта прямая называется общим перпендикуляром к двум скрещивающимся прямым. Длина этого перпендикуляра называется расстоянием между скрещивающимися прямыми.

Доказательство:

Пусть АВ и А’В’ – данные скрещивающиеся прямые.

Через них можно провести параллельные плоскости α и b. Любая прямая, перпендикулярная одновременно, к прямым АВ и А’В’ перпендикулярна и плоскости α. Множество перпендикуляров к плоскости α, которые пересекают АВ – есть некоторая плоскость g. Множество перпендикуляров к плоскости α и пересекающих А’В’ есть плоскость p. Обе эти плоскости перпендикулярны плоскости α и пересекаются по прямой НН’ которая также ^ α. Эта прямая искомая, и притом единственная.

Многогранный угол.

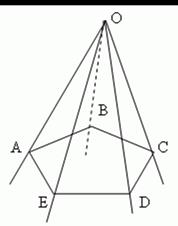Если через точку O провести множество плоскостей AOB, BOC, COD и т.д., которые последовательно пересекаются друг с другом по прямым OB, OC, OD и т.д. ( последняя из них EOA пересекается с первой AOB по прямой OA ), то мы получим фигуру, называемую многогранным углом. Точка O называется вершиной многогранного угла. Плоскости, образующие многогранный угол (AOB, BOC, COD, …, EOA), называются его гранями; прямые, по которым последовательно пересекаются грани ( OA, OB, OC, … , OE ) называются рёбрами многогранного угла. Углы AOB, BOC, COD, … , EOA называются его плоскими углами. Минимальное количество граней многогранного угла равно 3

Многогранный угол называется выпуклым, если он целиком расположен по одну сторону плоскости любой из его граней. В противном случае он называется вогнутым.

Теорема: Во всяком трехгранном угле любой плоский угол меньше суммы двух других.

Доказательство.

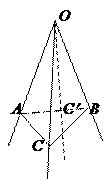Пусть дан трехгранный угол ÐОABC и для определенности пусть ÐAОB больше ÐAОC. В грани AОB построим угол ÐAОC’ равный по вершине ÐAОC

Через точки C и C’ проведем плоскость, пересекающую ребра ОA и ОB в точках A и B, где возьмем точку C’ так, чтобы ОC’ = ОC.

Имеем: AB<AC<BC

D AC’О =D AОC Þ AC = AC’. Тогда AB-AC<AC+CB-AC

Тогда BC’<CB

Тогда из D ОBC и D ОBC’ имеющих общую сторону ОB и BC’< BC Þ ÐCОB > ÐC’ОB

К обеим частям прибавим Ð AОC

ÐCОB + ÐAОC > ÐC’ОB + ÐAОC

Отсюда ÐCОB + ÐAОC > ÐAОB

Теорема: Сумма плоских углов многогранного угла всегда меньше четырех прямых (углов).

Доказательство

1. Рассмотрим трехгранный угол OABС

Продолжим OC за вершину O. Получим луч SC’.

Имеем новый трехгранный угол OC’AB в котором Ð C’SB + ÐC’SA > ÐBSA.

ÐBSA < ÐC’SB + ÐC’SA= 180°- ÐCSB +180° - ÐCSA

Отсюда

ÐBSA + ÐCSB + ÐCSA <4d=360 °

2.Случай многогранного угла постепенно сводится к случаю трехгранного угла:

С этой целью продолжают две грани смежных с одной и той же гранью так, что число граней уменьшается на 1. И так далее, пока не придем к трехгранному углу. В результате сумма плоских углов данного многогранного угла оказывается меньше суммы плоских углов полученного многогранного угла. Полученный многогранный угол постепенно преобразуем в трехгранный, а по первой части доказательства его сумма плоских углов < 4d, а значит и сумма плоских углов данного многогранного угла < 4d. .

Трехгранный угол называется равнобедренным, если 2 плоских угла его равны.