Плотность вероятности

Непрерывная случайная величина может быть задана не только с помощью функции распределения. Введем понятие плотности вероятности непрерывной случайной величины.

Рассмотрим вероятность попадания непрерывной случайной величины на интервал [х, х + Δх]. Вероятность такого события

P(х ≤ X ≤ х + Δх) = F(х+ Δх) – F(х),

т.е. равна приращению функции распределения F(х) на этом участке. Тогда вероятность, приходящаяся на единицу длины, т.е. средняя плотность вероятности на участке от х до х+ Δх, равна

.

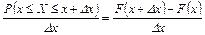Переходя к пределу Δх → 0, получим плотность вероятности в точке х:

,

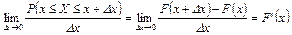представляющую производную функции распределения F(х). Напомним, что для непрерывной случайной величины F(х) – дифференцируемая функция.

Определение. Плотностью вероятности(плотностью распределения) f(x) непрерывной случайной величины Х называется производная ее функции распределения

Про случайную величину Х говорят, что она имеет распределение с плотностью f(x) на определенном участке оси абсцисс.

Плотность вероятности f(x), как и функция распределения F(x) является одной из форм закона распределения. Но в отличие от функции распределения она существует только для непрерывных случайных величин.

Плотность вероятности иногда называют дифференциальной функцией или дифференциальным законом распределения. График плотности вероятности называется кривой распределения.

Пример 4.4. По данным примера 4.3 найти плотность вероятности случайной величины Х.

Решение. Будем находить плотность вероятности случайной величины как производную от ее функции распределения f(x) = F'(x).

◄

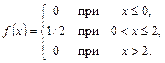Отметим свойства плотности вероятности непрерывной случайной величины.

1. Плотность вероятности – неотрицательная функция, т.е.

как производная монотонно неубывающей функции F(x).

2. Вероятность попадания непрерывной случайной величины Х в интервал [α, β,] равна определенному интегралу от ее плотности вероятности в пределах от α до β, т.е.

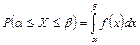
(4.10)

Геометрически вероятность попадания в интервал [α, β,] равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на отрезок [α, β,] (рис.4.4).

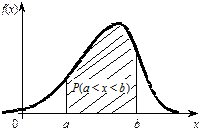
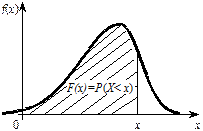
Рис. 4.4 Рис. 4.5

3. Функция распределения непрерывной случайной величины может быть выражен через плотность вероятности по формуле:

.

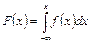(4.11)

Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения и лежащей левее точки х (рис. 4.5).

4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:

.

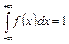(4.12)

Геометрически свойства 1 и 4 плотности вероятности означают, что ее график – кривая распределения – лежит не ниже оси абсцисс, а полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

Пример 4.5. Функция f(x) задана в виде:

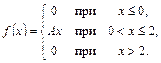
Найти: а) значение А; б) выражение функции распределения F(х); в) вероятность того, что случайная величина Х примет значение на отрезке [0; 1].

Решение. а) Для того, чтобы f(x) была плотностью вероятности некоторой случайной величины Х, она должна быть неотрицательна, следовательно, неотрицательным должно быть и значение А. С учетом свойства 4 находим:

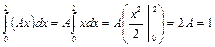, откуда А = .

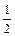б) Функцию распределения находим, используя свойство 3:

Если x ≤ 0, то f(x) = 0 и, следовательно, F(x) = 0.

Если 0 < x ≤ 2, то f(x) = х/2 и, следовательно,

.

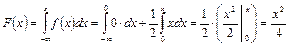Если х > 2, то f(x) = 0 и, следовательно

.

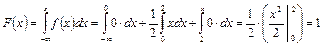в) Вероятность того, что случайная величина Х примет значение на отрезке [0; 1] находим, используя свойство 2:

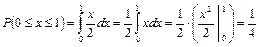= 0,25. ◄