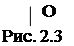Момент силы относительно оси

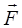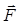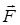Пусть на тело действует сила . Примем для простоты, что сила лежит в плоскости, перпендикулярной некоторой прямой ОО (рис. 2.2,a), которую назовем осью (например, это ось вращения тела). На рис. 2.2,a, А - точка приложения силы , О¢ - точка пересечения оси с плоскостью, в которой лежит сила; 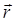- радиус-вектор, определяющий положение точки А относительно точки О¢; О¢B = b - плечо силы. Плечом силы относительно оси называется расстояние от оси до линии, вдоль которой действует сила; a - угол между векторами и .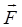

Моментом силы относительно оси ОО называется вектор, определяемый равенством

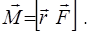(2.6)

Модуль этого вектора M = F r 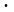Sin a = Fb. Иногда поэтому говорят, чтомомент силы относительно оси - это произведение силы на ее плечо.

Если сила направлена произвольно, то ее можно разложить на две составляющие: 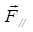и 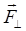(рис. 2.2,б), т.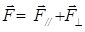е., , где 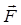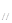- составляющая, направленная параллельно оси ОO, а 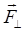лежит в плоскости, перпендикулярной оси. В этом случае под моментом силы 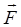относительно оси ОО понимают вектор

. (2.7)

В соответствии с выражениями (2.6) и (2.7) вектор направлен вдоль оси (cм. рис.2.2, а).

Момент импульса тела относительно оси вращения

Пусть тело вращается вокруг некоторой оси ОО с угловой скоростью w. Разобьем это тело мысленно на элементарные участки с массами Dm₁, Dm₂,...Dm_i,..., которые находятся от оси соответственно на расстояниях Dr_1, Dr₂,..., Dr₃, ..., и вращаются по окружностям, имея линейные скорости v₁, v₂, ..., v_i, ... Известно, что величина, равная 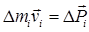- есть импульс i- го участка. Моментом импульса i- го участка (материальной точки) относительно оси вращения называется вектор (точнее, псевдовектор)

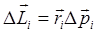, (2.8)

где 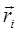- радиус-вектор, определяющий положение i-го участка относительно оси.

Моментом импульса всего тела относительно оси вращения называют вектор:

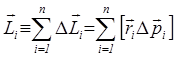, (2.9)

модуль которого .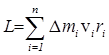

В соответствии с выражениями (2.8) и (2.9) векторы 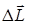и 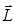направлены по оси вращения (рис.2.3). Легко показать, что момент импульса тела относительно оси вращения и момент инерцииI этого тела относительно той же оси связаны соотношением

.(2.10)