Момент инерции тела относительно оси

Пусть имеется твердое тело. Выберем некоторую прямую ОО (рис.2.1), которую будем называть осью (прямая ОО может быть и вне тела).

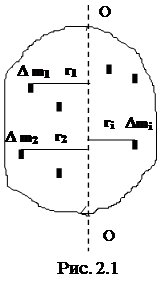
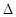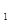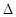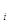Разобьем тело на элементарные участки (материальные точки) массами m , m ,..., m , находящиеся от оси на расстоянии соответственно r , r 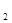,... r 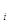,... . Моментом инерции материальной точки относительно оси (OO) называется произведение материальной точки на квадрат ее расстояния до этой оси:

DI_i = Dm_i 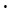r_i². (2.1)

Моментом инерции (МИ) тела относительно оси (ОО) называется сумма произведений масс элементарных участков тела на квадрат их расстояния до оси:

I = .(2.2)

Как видно, момент инерции тела есть величина аддитивная - момент инерции всего тел относительно некоторой оси равен сумме моментов инерции отдельных его частей относительно той же оси.

В данном случае 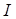= 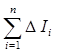. Измеряется момент инерции в кг×м .

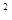Так как

Dm_i = r DV_i (2.3)

где r - плотность вещества; DV 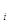- объем - i - го участка, то

I =

или, переходя к бесконечно малым элементам,

I= 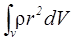(2.4)

Формулу (2.4) удобно использовать для вычисления МИ однородных тел правильной формы относительно оси симметрии, проходящей через центр масс тела. Например, для МИ цилиндра относительно оси, проходящей через центр масс и параллельно образующей цилиндра, эта формула дает

,

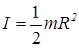где m - масса; R - радиус цилиндра.

Большую помощь при вычисления МИ тел относительно некоторых осей оказываеттеорема Штейнера: МИ тела I относительно любой оси равен сумме МИ этого тела I_с относительно оси, проходящей через центр масс тела и параллельно данной, и произведения массы тела на квадрат расстояния d между указанными осями:

I = I_с+ m d².(2.5)