Интеграл от разрывной функции.

Пусть функция 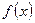определена и непрерывна при 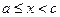, а при x = c функция либо не определена, либо имеет разрыв.

Определение. Интеграл 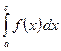от функции 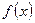, разрывной в точке c, определяется следующим образом:

.

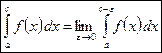Если предел, стоящий справа, существует, то интеграл называется несобственным сходящимся интегралом, в противном случае интеграл называется расходящимся.

Пример:

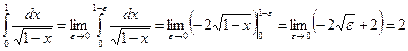
Если функция 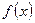имеет разрыв в левом конце отрезка [a;c] (т.е. при x = a), то по определению:

.

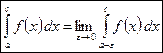Если функция 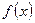имеет разрыв в некоторой точке 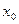внутри отрезка [a;c], то

,

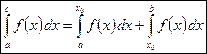если оба несобственных интеграла, стоящих в правой части равенства, существуют.

Пример:

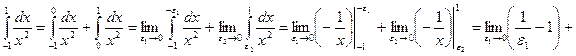
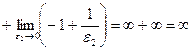
Таким образом, 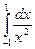расходится.

Замечание. Если функция 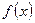, определённая на отрезке [a;b], имеет внутри этого отрезка конечное число точек разрыва 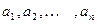, то интеграл от функции 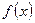на отрезке [a;b] определяется следующим образом:

,

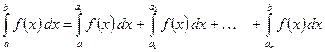если каждый из несобственных интегралов в правой части равенства сходится. Если хотя бы один из этих интегралов расходится, то и 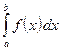называется расходящимся.

Тема 15. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА