Формула Ньютона-Лейбница
Пусть в определённом интеграле  нижний предел
нижний предел 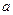 зафиксирован, а верхний предел
зафиксирован, а верхний предел 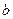 меняется. Тогда будет меняться и значение интеграла, т.е. интеграл есть функция верхнего предела. Обозначим эту функцию через
меняется. Тогда будет меняться и значение интеграла, т.е. интеграл есть функция верхнего предела. Обозначим эту функцию через 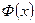 :
:
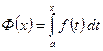 .
.
Теорема 1. Если 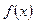 – непрерывная функция и
– непрерывная функция и 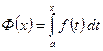 , то имеет место равенство
, то имеет место равенство 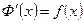 .
.
Иными словами, производная от определённого интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела.
Замечание. Из теоремы 1 следует, что всякая непрерывная функция имеет первообразную. Действительно, если функция 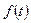 непрерывна на отрезке
непрерывна на отрезке 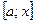 , то определённый интеграл
, то определённый интеграл 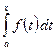 существует, т.е. существует функция
существует, т.е. существует функция 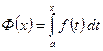 , но по теореме 1 она является первообразной от
, но по теореме 1 она является первообразной от 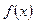 .
.
Теорема 2. Если 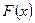 есть какая-либо первообразная от непрерывной функции
есть какая-либо первообразная от непрерывной функции 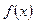 , то справедлива формула
, то справедлива формула
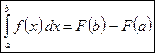 .
.
Эта формула называется формулой Ньютона-Лейбница.
Доказательство: Пусть 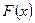 есть первообразная от
есть первообразная от 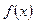 . По теореме 1
. По теореме 1 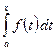 есть также первообразная от
есть также первообразная от 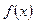 . Следовательно,
. Следовательно,
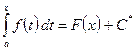
(так как любые две первообразные от данной функции отличаются на постоянную 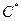 ).
).
Пусть x=a, тогда
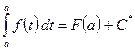 ,
,
т.е.
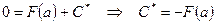 .
.
Получаем
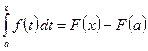 .
.
При x=b получим формулу Ньютона-Лейбница:
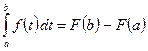
или
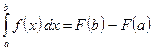 .
.
Пример: 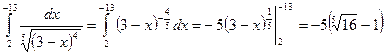 .
.
Дата добавления: 2022-05-27; просмотров: 79;










