Уравновешивание вращающихся тел
Задача об уравновешивании вращающихся тел состоит в таком выборе их масс, при котором произойдёт полное или частичное погашение добавочных инерционных давлений на опоры.
Результирующая центробежная сила инерции:
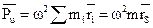
Результирующий момент всех сил инерции тела относительно плоскости, проходящей через центр масс.
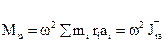 ,
,
где m – масса всего тела, 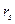 - расстояние центра S масс тела от оси вращения;
- расстояние центра S масс тела от оси вращения; 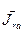 - центробежный момент инерции относительно оси вращения и плоскости, перпендикулярной к оси вращения и проходящей через центр S масс тела.
- центробежный момент инерции относительно оси вращения и плоскости, перпендикулярной к оси вращения и проходящей через центр S масс тела.
При вращение тела угол между векторами 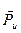 и
и 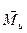 сохраняет всё время одно и тоже значение
сохраняет всё время одно и тоже значение 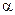 . Если результирующая сила инерции
. Если результирующая сила инерции 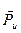 и результирующий момент
и результирующий момент 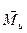 сил инерции равны нулю, тогда тело будет полностью уравновешенным, а значит вращающееся тело не оказывает никаких динамических давлений на опоры.
сил инерции равны нулю, тогда тело будет полностью уравновешенным, а значит вращающееся тело не оказывает никаких динамических давлений на опоры.
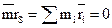
| (4.1) | |
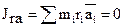
| (4.2) |
Эти условия будут выполняется только тогда, когда центр масс тела будет лежать на оси вращения, которая будет являться одной из его главных осей инерции. Если одновременно выполняются равенства (4.1) и (4.2), то центробежный момент инерции 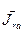 будет равен нулю. Если выполняется (4.1) условие, то тело считается уравновешенным статически, если выполняется (4.2) условие, то тело считается уравновешенным динамически.
будет равен нулю. Если выполняется (4.1) условие, то тело считается уравновешенным статически, если выполняется (4.2) условие, то тело считается уравновешенным динамически.
Статический дисбаланс 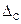 измеряется статическим моментом.
измеряется статическим моментом.
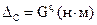
| (4.3) |
G – вес вращающегося тела, н.
Динамический дисбаланс 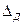 вращающегося тела измеряется величиной
вращающегося тела измеряется величиной
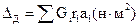
| (4.4) |
На практике неуравновешенное тело уравновешивают при помощи противовесов. Вращающиеся тела, у которых общая длина а значительно меньше их диаметра, имеют незначительные центробежные моменты инерции 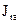 ; поэтому такие тела достаточно уравновесить только статически.
; поэтому такие тела достаточно уравновесить только статически.
Предположим, что тело А статически неуравновешенно. В простейшем случае противовес помещают на линии, проходящей через центр тяжести S, по другую сторону от оси вращения на расстоянии 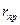 от неё. (рис. 4.1)
от неё. (рис. 4.1)
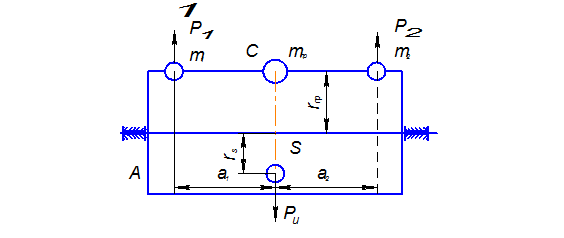
Рис. 4.1
Массу 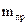 противовеса находим из уравнения (4.1) :
противовеса находим из уравнения (4.1) :
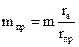
| (4.5) |
Вместо установки противовеса можно удалить часть массы. Величина удаляемой массы определяется по формуле (4.5). Иногда плоскость крепления противовеса не может быть выбрана конструктивно в той плоскости вращения, в которой расположены неуравновешенные массы. В этом случае можно установить два противовеса в двух перпендикулярных к оси вращения плоскостях, обычно называемых плоскостями исправления, но при этом необходимо исключить возможность появления давления на опоры не только от результирующей силы инерции, но и от моментов сил инерции. Массы 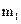 и
и 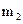 противовесов определяем вы соответствии с формулами (4.1) и (4.2) из уравнений
противовесов определяем вы соответствии с формулами (4.1) и (4.2) из уравнений
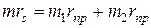
и
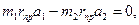
откуда
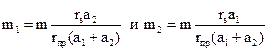
| (4.6) |
Сложив массы этих противовесов, получим
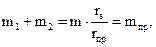
а из их отношения найдём
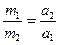
Полное уравновешивание вращающегося тела может быть достигнуто также при помощи двух противовесов, расположенных в произвольно выбранных плоскостях 1 и 2 и на произвольных расстояниях от оси вращения.
Вращающиеся тела обычно выполняют так, чтобы они были уравновешены сами по себе. Чаще всего вращающиеся тела выполняют в форме одного или нескольких цилиндров, имеющих общую ось, совпадающую с осью вращения тела. Однако во многих случаях такая форма не может быть выполнена и вращающееся тело без противовесов является неуравновешенным. Для определения величины и положения противовесов необходимо по чертежу выделить уравновешенную часть тела и определить для оставшихся частей – колен, кулачков и т.д. центры тяжести их, считая, что в них сосредоточены массы этих частей.
Предположим, что для какого-либо тела все его неуравновешенные массы свелись к трём неуравновешенным массам (рис. 4.2). Пользуясь методом приведения вектора к заданному центру, можно любое число вращающихся в различных плоскостях масс уравновесить двумя противовесами. Пусть центры тяжести масс 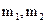 и
и 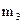 расположены в трёх плоскостях, перпендикулярных к оси вращения. Условия отсутствия давления на подшипники от главного вектора и главного момента относительно центра приведения О1 центробежных сил инерции выражаются уравнениями:
расположены в трёх плоскостях, перпендикулярных к оси вращения. Условия отсутствия давления на подшипники от главного вектора и главного момента относительно центра приведения О1 центробежных сил инерции выражаются уравнениями:
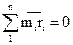
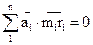
Строим многоугольники векторов сил и векторов моментов (рис. 4.2г,д). Уравновешивающим в первом случае является вектор 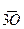 , изображённый в плоскости 2 вектором
, изображённый в плоскости 2 вектором 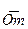 ,(рис. 4.2 в) а во втором – вектор
,(рис. 4.2 в) а во втором – вектор 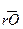 (рис. 4.2 д), изображающий повёрнутый момент пары векторов
(рис. 4.2 д), изображающий повёрнутый момент пары векторов 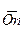 , расположенного в плоскости 1, и
, расположенного в плоскости 1, и 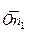
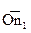 , расположенного в плоскости 2. Каждый из них равен по величине
, расположенного в плоскости 2. Каждый из них равен по величине 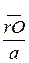 . Таким образом, заданные массы
. Таким образом, заданные массы 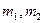 и
и 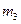 будут полностью уравновешены двумя массами, расположенными вдоль
будут полностью уравновешены двумя массами, расположенными вдоль 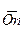 в плоскости 1 и вдоль равнодействующей
в плоскости 1 и вдоль равнодействующей 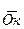 в плоскости 2. Из изложенного следует, что:
в плоскости 2. Из изложенного следует, что:
1.) любое количество вращающихся масс, расположенных в одной плоскости вращения, уравновешивается одним противовесом, находящимся в той же плоскости, при соблюдении условия равновесия
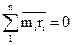
| (4.7) |
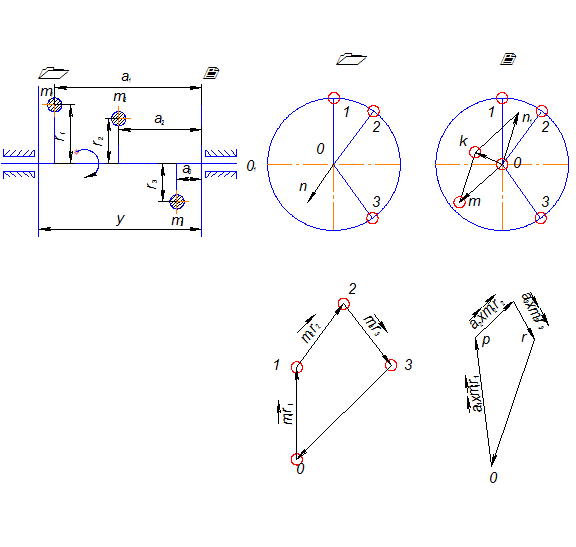
Рис. 4.2
2.) любое количество масс, лежащих в разных плоскостях вращения, уравновешивается двумя противовесами, установленными в двух произвольных плоскостях, перпендикулярных к оси вращения, при соблюдении двух условий равновесия:
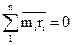
| (4.8) |
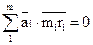
Дата добавления: 2021-12-14; просмотров: 467;











