Силовой анализ зубчатых механизмов

Для подавляющего большинства зубчатых передач основным является установившийся режим работы. Поэтому в передачах этого типа моменты от сил инерции будут равны нулю (без учета колебаний, вызываемых переменной жесткостью и ошибками шага).

Давление между эвольвентными профилями передается по линии зацепления, которая совпадает с их общей нормалью.

Если к ведомому колесу приложен момент сопротивления M_C, то сила сопротивления:

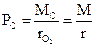
Сила P_C приложена к ведущему колесу 1; ведомому колесу 2 приложена движущая сила 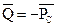. Из формулы следует, что, если 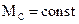, то сила P_C давления между зубьями постоянна как по величине, так и по направлению; она увеличивается с увеличением угла зацепления.

В центре ведущего колеса 1 приложим две равные и противоположно направленные силы P_C. Силы R^* — давление в опорах колеса; две другие силы R образуют пару сил, момент которой равен моменту M_Д. Подставляя значение P_C из формулы, получаем

.

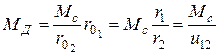Пара 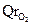, приложенная к колесу 2, преодолевает приложенный к этому колесу момент сопротивления M_C.

Равные и обратно направленные силы R^* и Q^* образуют пару с моментом

.

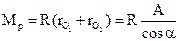Эта пара стремится повернуть стойку (раму) передачи (в нашем случае по часовой стрелке). Для того чтобы этого не произошло, стойка должна быть закреплена. Момент, создаваемый рассматриваемой парой, получил название реактивного момента.

Очевидно, что и при переменном M_C направления сил давления между зубьями и в опорах валов будут постоянны. Это является одним из преимуществ эвольвентного зацепления, так как обеспечивает спокойную работу передачи.

Так как профили зубьев в процессе их зацепления имеют относительное скольжение, то между ними возникают силы трения, равнодействующая F которых направлена против скорости скольжения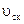

Величина этой силы

,

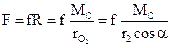где f - коэффициент трения скольжения профилей.

Мощность сил трения в наружном зацеплении

.

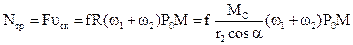Следовательно, мощность сил трения в зацеплении переменна и увеличивается по мере того, как точка M касания профилей удаляется от полюса зацепления.

В опорах валов также возникают силы трения, пропорциональные давлениям R и Q в этих опорах. Величины этих сил трения зависят от ряда факторов (от условий смазки соприкасающихся поверхностей, от их упругих свойств, определяющих закон распределения удельных давлений, от скорости скольжения опорных поверхностей и т. д.). Равнодействующая этих сил 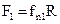, где f_n1 - коэффициент трения, учитывающий условия работы вала в подшипниках. Приложена эта сила в одной из точек опорной поверхности вала на расстоянии r_B от его оси.

Мощность сил трения в опорах

;

.

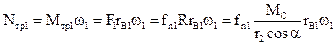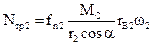Из формул видно, что если 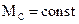, то и мощность сил трения в опорах постоянна.

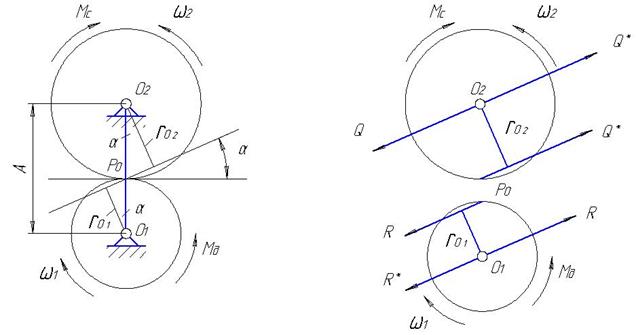
Рис. 3.17

Пользуясь этой формулой, можно определить момент M_Д и мощность N_Д двигателя, который должен быть соединен с ведущим валом передачи, если заданы M_C и i₁₂

Величины коэффициентов f и f_n зависят от большого числа различных факторов и могут колебаться в очень широких пределах. Например, коэффициенты трения профилей зависят не только от материалов и точности их обработки, но и от смазки; кроме трения скольжения, между профилями имеет место трение качения; если передача работает в масляной ванне, то затрачивается работа на перемешивание масла и т. д.

6.2. Определение моментов в планетарном механизме без учета трения

Рассмотрим вопрос определения моментов в планетарном механизме, звенья которого вращаются равномерно. В планетарном механизме изображенном на (рис. 3.18) солнечное колесо 1, водило 2 и коронное колесо 4 вращаются вокруг центральной оси С. Тангенциальная составляющая Р₃₁ реакции на сателлит 3 со стороны солнечного колеса 1 без учета силы трения приложена в полюсе зацепления А. В обратную сторону направлена сила Р₁₃. В точке В действуют составляющие реакции Р₃₄ и Р₄₃, а в центре сателлита – Р₂₃ и Р₃₂.

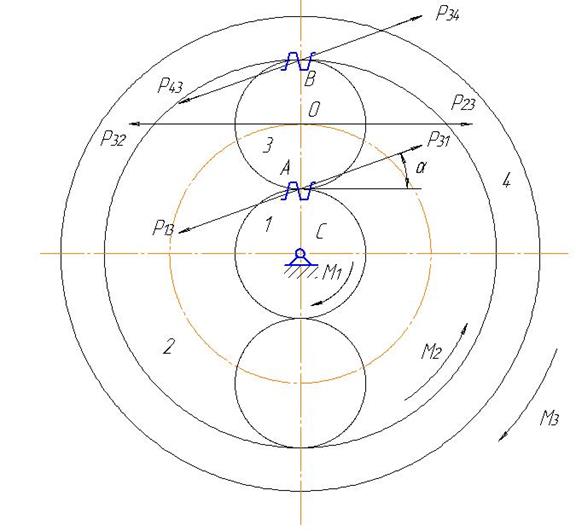
Рис.3.18

Будем рассматривать такие планетарные механизмы, в которых сателлит не является выходным звеном, т.е. М₃=0. Тогда 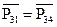и потому:

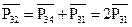
(3.15)

Рассматривая равновесие звена 1, получим:

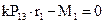
откуда

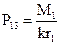
(3.16)

где k – количество сателлитов механизма.

Из равновесия звена 2 имеем: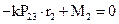

Откуда

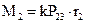
(3.17)

Учитывая (3.15) и (3.16), перепишем (3.17):

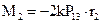
из (3.17) и (3.16) получим:

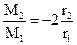
(3.18)

Запишем условие равновесия звена 4:

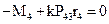
Откуда

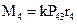
(3.19)

Поэтому, учитывая условие: Р₄₃= –Р₁₃ из (3.19) имеем:

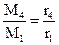
Следовательно, если один из моментов, действующих в планетарном механизме, известен, то зная радиусы начальных окружностей, по формулам (3.18) и (3.19) можно определить неизвестных моменты.

Задачу определения моментов можно решить и с помощью общего плана угловых скоростей. Рассмотрим методику определения моментов.

Пусть для планетарного редуктора с корригированными зубчатыми колесами построен общий план угловых скоростей (рис. 3.19)

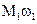– мощность, подводимая к звену 1.

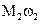– мощность, снимаемая с водила.

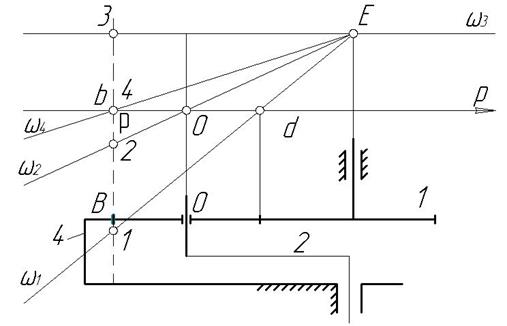
Рис. 3.19

Так как потери не учитываются, то:

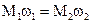
но

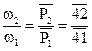
поэтому

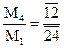
(3.20)

Так как под действием моментов, планетарный механизм в установившемся равновесном режиме находится в равновесии, то имеет место равенство

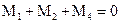
(3.21)

где М₄, при 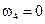следует понимать как момент, который необходимо приложить к звену 4, чтобы удержать его от вращения.

Из (3.21) получим:

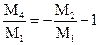
(3.22)

Учитывая (3.21) перепишем (3.22) так:

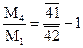
или после упрощения:

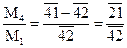
Окончательно получим:

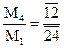
Из (3.21) и (3.22) следует правило для определения моментов.

6.3. Определение коэффициента полезного действия планетарного механизма

К.п.д. механической передачи зависит от многих факторов, из которых наибольшее значение имеют потери мощности в зацеплении пар зубчатых колес. Определим к.п.д. планетарного редуктора при передаче моментов от звена 1 к звену 2 по формуле:

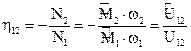
(3.23)

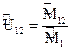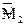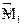где называется силовым передаточным отношением. Здесь и – моменты, действующие на звенья 2 и 1 с учетом трения в зацеплении 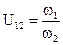– кинематическое передаточное отношение.