Силовой анализ механизмов. Определение реакций в кинематических парах
Силовой анализ механизмов основывается на решении прямой, или первой, задачи динамики - по заданному движению определить действующие силы. Поэтому законы движения начальных звеньев при силовом анализе считаются заданными. Внешние силы, приложенные к звеньям механизма, обычно тоже считаются заданными и, следовательно, подлежат определению только реакции в кинематических парах. Но иногда внешние силы, приложенные к начальным звеньям, считают неизвестными. Тогда в силовой анализ входит определение сил, при которых выполняются принятые законы движения начальных звеньев. При решении обеих задач используется принцип Д'Аламбера, согласно которому звено механизма может рассматриваться как находящееся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции. Уравнения равновесия в этом случае называют уравнениями кинетостатики, чтобы отличить их от обычных уравнений статики, т. е. уравнений равновесия без учета сил инерции. Обычно звенья плоских механизмов имеют плоскость симметрии, параллельную плоскости движения. Тогда главный вектор сил инерции звена Pu и главный момент сил инерции звена 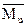 , определяются по формулам:
, определяются по формулам:
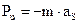
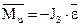 ,
,
где m- масса звена;
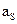 - вектор ускорения центра масс.
- вектор ускорения центра масс.
При кинетостатическом расчете механизма необходимо определить реакции в кинематических парах и либо уравновешивающую силу, либо уравновешивающий момент пары сил.
Силовой расчет механизмов будем вести в предположении, что трение в кинематических парах отсутствует, и все силы, действующие на механизм, расположены в одной плоскости.
Одним из известных методов силового расчета является метод рассмотрения каждого звена механизма в равновесии. При этом методе механизм расчленяется на отдельные звенья.
Вначале рассматривается равновесие крайнего звена, считая от главного (ведущего), затем равновесие звена, соединенного с крайним, и т.д. Равновесие главного звена рассматривается в последнюю очередь.
Рассматривая отдельно взятое звено в равновесии, необходимо приложить к нему все внешние силы (PДВ, РПС ,РИ ,G) включая реакции связей, с которыми отсоединенные звенья действуют на взятое звено.
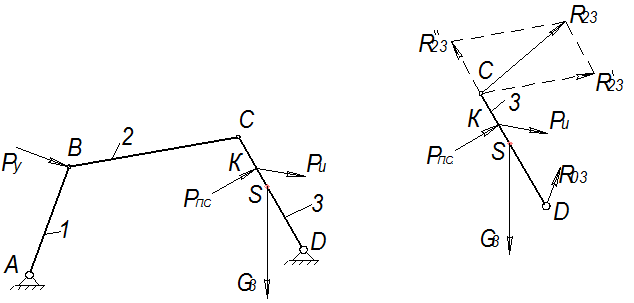
Изложим методику расчета на примере четырехзвенного механизма. Вначале рассмотрим в равновесии звено 3 (коромысло), приложив к нему все действующие силы, включая реакции связей. (Рис. 3.7)
| |
| а | б |
| Рис. 3.7 |
Реакция во вращательной паре “С” неизвестна ни по величине, ни по направлению.
Для определения этой реакции заменяем её двумя составляющими
(рис. 7б), одну из которых – 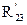 направляем по шатуну (2), вторую составляющую
направляем по шатуну (2), вторую составляющую 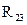 –
– 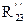 – по коромыслу (3).
– по коромыслу (3).
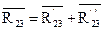
Величина 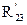 может быть найдена из условия равновесия рассматриваемого звена.
может быть найдена из условия равновесия рассматриваемого звена.
Звено (3) находится в равновесии под действием следующих сил РП.С.; Риз; G3; R03; 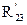 ;
; 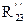 .
.
Составляем уравнение моментов всех сил относительно точки D
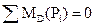
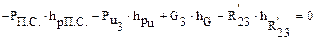
откуда
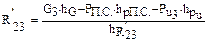
Если после определения этой величины она окажется отрицательной, то её направление будет противоположно выбранному.
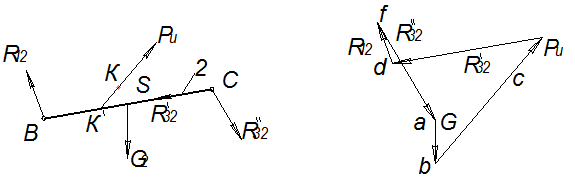
Составляющую 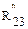 можно найти, рассмотрев в равновесии отдельно взятое звено (2) (рис. 3.8а).
можно найти, рассмотрев в равновесии отдельно взятое звено (2) (рис. 3.8а).
| |
| а | б |
| Рис. 3.8 |
Из условия равновесия звена (2) можно написать
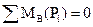
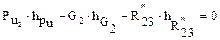
причем 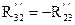
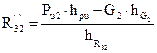
Оставшуюся неизвестную реакцию R12 можно найти графическим методом, построив план сил этого звена (рис. 3.8б).
Уравнение равновесия звена (2) имеет следующий вид:
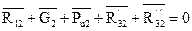
Из произвольно выбранного полюса 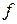 откладываем в масштабе
откладываем в масштабе 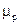 силу
силу 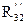 в виде вектора
в виде вектора 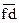 , к нему геометрически прибавляем вектор
, к нему геометрически прибавляем вектор 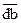 , изображающий в том же масштабе
, изображающий в том же масштабе 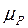 силу G и т.д.
силу G и т.д.
Вектор  дает нам величину реакции R12 в масштабе
дает нам величину реакции R12 в масштабе 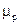 .
.
Далее приступаем к нахождению силы, уравновешивающей механизм.
Для этого рассматриваем в равновесии кривошип AB. (рис. 3.9).
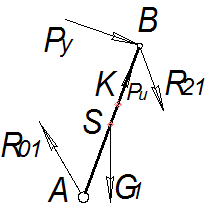
Рис. 3.9
Кривошип находится под действием силы веса G1, реакции шатуна (2) на кривошип R21, силу инерции Pu1.
Под действием этих сил кривошипы в общем случае не будет находиться в равновесии. Для равновесия необходимо приложить уравновешивающую силу Рy, или уравновешивающий момент Мy.
Этими уравновешивающими силой и моментом являются реактивные силы или момент от двигателя.
Пусть уравновешивающая сила будет направлена по нормали к кривошипу и приложения в точке В. Из условия равновесия звена АВ, можно составить уравнение суммы моментов всех сил относительно точки А.
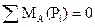
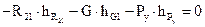
откуда
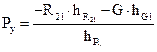 ;
;
Уравновешивающую силу можно найти также методом, при котором в равновесии рассматривается весь механизм.
Условие равновесия механизма можно выразить следующим уравнением:
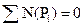
| (3.7) |
Сумма мощностей всех сил, приложенных к механизму, с учетом сил инерции и уравновешивающих сил равна нулю.
Мгновенная мощность силы, приложенной в i –той точке пропорциональна моменту этой силы относительно конца вектора повернутой скорости данной точки (рис. 3.10).
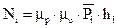
| (3.8) |
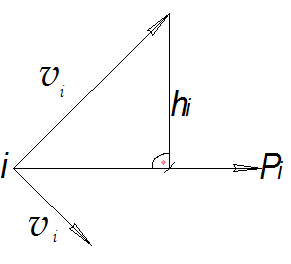
Рис. 3.10
Из уравнения равновесия можно найти уравновешивающую силу. Часто удобно находить Рy с помощью вспомогательного рычага Жуковского, когда для механизма построен полярный план скоростей, повернутый на 90°. В последнем случае к концам найденных векторов скоростей следует приложить действующие внешние силы.
После этого, рассматривая повернутый план скоростей как жесткий рычаг, вращающийся вокруг полюса Р можно написать уравнение равновесия рычага в виде суммы моментов сил относительно полюса:
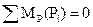
Уравнение равновесия плана скоростей, рассматриваемого как жесткий рычаг, тождественно уравнению мощностей.
Если к звеньям механизма кроме сил приложен еще и момент М (рис.11), то его можно рассматривать как пару сил, составляющая которой равна:
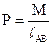 ё ё
| (3.11) |
Найденные силы Р прикладываются в соответствующих изображающих точках плана скоростей.
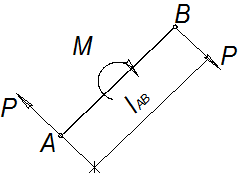
Рис. 3.11
Дата добавления: 2021-12-14; просмотров: 468;











