Расчет резьбовых соединений на прочность

Виды разрушения резьбовых крепежных деталей: разрыв стерж­ня по резьбе или переходному сечению у головки; повреждение или разрушение резьбы (смятие и износ, срез, изгиб); повреждение головки болта (винта).

Размеры стандартных болтов, винтов и шпилек отвечают условию равнопрочности всех элементов соединения. Поэтому можно ограничиваться расчетом по одному, основному критерию – прочнос­ти нарезной части, а размеры винтов, болтов и гаек принимать по таблицам стандарта в зависимости от рассчитанного диаметра резь­бы. Длину болта, винта и шпильки выбирают в зависимости от тол­щины соединяемых деталей.

Рассмотрим расчет на прочность резьбовых соединений при по­стоянной нагрузке.

Болт нагружен внешней силой F (болт без предварительной затяжки), например, нарезанный участок крюка для подвешивания груза. Опасным является сечение крюка, ослабленное нарезкой (рис. 26.21). Из условия прочности на растяжение

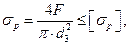(26.22)

откуда

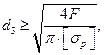(26.23)

где 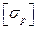=0.6 – допускаемое напряжение при растяжении болта из углеродистой стали.

Болт затянут силой затяжки F_з, а внешняя нагрузка отсут­ствует (ненагруженные крышки, кронштейны и т.п.). Стержень бол­та испытывает совместное действие растяжения и кручения, т.е. растягивается осевой силой F₃ от затяжки болта и скручивается моментом, равным моменту сил трения в резьбе T_p (формула (26.16)), Прочность таких болтов (рис. 26.22) определяют по эквивалентному напряжению

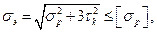(26.24)

где 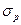– напряжение от растяжения, определяемое по формуле (26.22) при F=F_з; 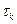– напряжение от кручения, 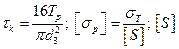– требуемый коэффициент запаса прочности болта, принимаемый в зависимости от материала

болта, характера нагрузки и диаметра болта.

Для стандартных метрических резьб , т. е. расчет болта на совместное действие растяжения и кручения можно заме­нить расчетом на растяжение, но по увеличенной в 1.3 раза силе F_р. Для метрических резьб

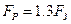(26.25)

Расчетный диаметр резьбы болта опреде­ляют по формуле (26.23), принимая

F = F_P.

Болтовое соединение нагружено си­лами, сдвигающими детали в стыке. Усло­вием надежности соединения является от­сутствие сдвига деталей в стыке.

В соединении с зазором (рис. 26.23 а) болт устанавливают с предвари­тельной затяжкой. Внешняя сила F непосредственно на болт не передается, поэтому его рассчитывают на растяжение по силе затяжки F_з.

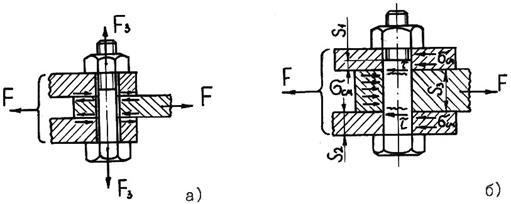
Рис. 26.23

Во избежание сдвига деталей при наличии зазора сила трения на поверхностях стыка должна быть не меньше внешней сдвигающей силы F:

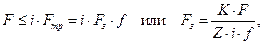(26.26)

где i – число стыков в соединении; f – коэффициент трения; K – коэффициент запаса (К = 1.3 – 1.5 при статической и К == 1.8 – 2.0 при переменной нагрузке); Z – число болтов в соеди­нении.

Болт в этом случае рассчитывают по силе затяжки

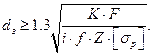(26.27)

При установке болта без зазора (рис. 26.23 б) предваритель­ная затяжка не требуется. Болт испытывает срез и смятие. Стер­жень болта рассчитывают на

срез, а при тонких деталях – и на смятие. Условия прочности:

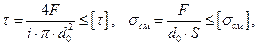(26.28)

где 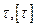–соответственно расчетное и допускаемое напряжения для материала болта на срез, 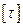= (0.2 – 0.3) 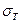; d_o – диа­метр ненарезанной части болта; 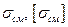–соответственно расчетное и наименьшее допускаемое напряжения смятия (для матери­ала болта или детали), 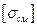= (0.8 – 1.0) 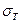; S–наименьшая толщина детали.

Болт затянут, а внешняя нагрузка стремится раскрыть стык (болты для крепления крышек резервуаров для газа и жидкости, на­груженные давлением выше атмосферного, крепления цилиндров, на­сосов, станин к фундаментам и др.). Затяжка болтов должна обес­печить герметичность соединения или нераскрытие стыка (не допус­тить появления зазора) под нагрузкой. Эта задача решается с уче­том деформации деталей соединения.

Внешняя нагрузка 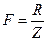(R – равнодействующая нагрузки; Z – число болтов) вызывает удлинение болта на 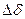(рис. 26.24), а деформация деталей уменьшается на ту же величину. Нагрузка со стороны деталей на болт также уменьшится. Именно поэтому счита­ют, что болт воспринимает часть внешней нагрузки .

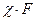Суммарная нагрузка на затянутый болт

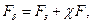(26.29)

где 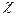–коэффициент внешней нагрузки, показывающий, какая часть внешней нагрузки воспринимается болтом (учитывает податливость болта и соединяемых деталей).

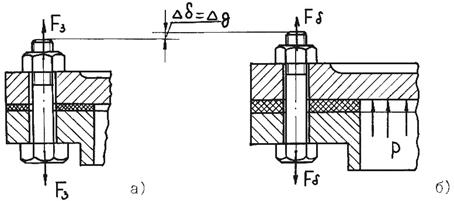
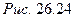
Величина 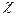–определяется по условию равенства дополнитель­ных деформаций болта и деталей

(26.30)

где 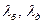– коэффициенты податливости соответственно болта и деталей, численно равные изменению их длины при действии силы, равной 1 H.

Из равенства (26.30) следует

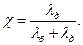
Точный расчет коэффициента 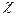сложен, а так как на практике величину затяжки болтов в большинстве случаев не контролируют, то смысл точного расчета теряется. При приближенных расчетах при­нимают: для соединений стальных и чугунных деталей без упругих прокладок 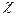= 0.2 – 0.3; для соединения тех же деталей, но с упругими прокладками (резина, полиэтилен, асбест, паронит и др.) 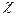= 0.4 – 0.5.

Предварительная затяжка болта F_з должна быть больше мини­мальной силы предварительной затяжки болта 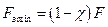. Из условия сохранения плотности стыка соединяемых деталей (невозможности образования зазора) принимают

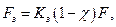(26.31)

где K_з – коэффициент запаса предварительной затяжки: при постоянной нагрузке K_з = 1.25 – 2.0; при переменной К_з = 2.5 – 4.

При расчете на прочность, если возможна последующая затяжка болта, его рассчитывают по расчетной нагрузке F_р с учетом кручения:

(26.32)

26.5.6. Расчет резьбовых соединений
при переменном режиме нагружения

Крепежные детали, работающие при переменном режиме нагружения, рассчитывают на усталость. Болты устанавливаются с предварительной затяжкой, при которой создается напряжение 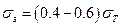. Вследствие этого циклическое изменение расчетной силы F_б значительно меньше по сравнению с изменением внешней силы F.

Расчет на усталость ведут как проверочный по двум коэффициентам запаса прочности: по амплитуде цикла и по наибольшему напряжению цикла (рис. 26.25). Предварительно болт рассчитывают из условия его статической прочности с учетом формул (26.29) или (26.32).

Коэффициент запаса прочности по амплитуде цикла

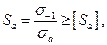(26.33)

где 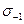– предел выносливос­ти материала болта (шпильки); – амплитуда переменных напряжений 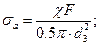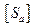– требуемый коэффициент запаса прочности по амплитуде [S_a]= 2.5 – 4.0.

Коэффициент запаса по наибольшему напряжению цикла

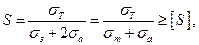(26.34)

где [S] = 1.25 – 2.5.

При S_a ≥ [S_a] и S ≥ [S] болт удовлетворяет условию проч­ности при действии переменных напряжений.

За счет уменьшения коэффициента внешней нагрузки может быть повышена прочность резьбового соединения при переменных нагруз­ках. Это может быть достигнуто уменьшением податливости стыка и увеличением податливости болта, в частности диаметр стержня бол­та уменьшают до диаметра d₃.

Литература

1. Аркуша А.И. Руководство к решению задач по теоретической механике– М.: Высш. школа, 1989; 1990; 1999.

2. Артоболевский И. И. Теория механизмов и машин. – М.: Машиностроение, 1975. – 639 с.

3. Артоболевский И.И., Эдельштейн Б.В. Сборник задач по те­ории механизмов и машин. – М.: Машиностроение, 1975. – 256 с.

4. Беляев Н. М. Сопротивление материалов. – М.: Наука, 1976. – 608 с.

5. Гернет М.М. Курс теоретической механики. – М.: Высшая шко­ла, 1970.– 440 с.

6. Дубейковский Е. Н., Савушкин Е. С. Сопротивление материалов: Учеб. пособие для машиностр. спец. техникумов. – М.: Высшая школа, 1985. –192 с.

7. Иосилевич Г. Б., Строганов Г. Б., Маслов Г. С. Прикладная механика: Учеб. для вузов/ Под ред. Г. Б. Иосилевича. – М.: Высшая школа, 1989. –360с.

8. Ицкович Г. М., Винокуров А. И., Барановский Н. В. Сборник задач по сопротивлению материалов: Учеб. пособие. – 4-е изд. – Л.: Судостроение, 1972.

9. Каленик В. В., Акулич В. К. Текст лекций по разделу «Теория механизмов и машин» курса «Прикладная механика» для студ. немеханических спец. – Мн.: БПИ, 1983.

10. Кильчевский Н. А., Ремизова Н. И., Шепелевская Н. Н. Основы теоретической механики. – Киев: Техника, 1968. – 260 с.

11. Кинасошвили Р. С. Сопротивление материалов. – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1975. – 384 с.

12. Методические указания по решению задач по курсу «Приклад­ная механика» для студентов немеханических специальностей/ А. А. Миклашевич, С. Е. Карпович, В. В. Каленик, Н. Н. Розанова. –
В 2 .ч. Ч 2. – Мн.: БПИ, 1985. – 37 с.

13. Мовкин М. С. Израелит А. Б. Теоретическая механика. – Л.: Судостроение, 1972.

14. Никитин Е. М. Теоретическая механика для техникумов. – М.: Наука, 1971 (и последующие издания).

15. Осадчий В. И., Фаин А. М. Руководство к решению задач по теоретической механике. – М.: Высш. школа, 1972.

16. Павловский М. А., Акинфиева Л. Ю., Бойчук О. Ф. Теоретическая механика. В 2 ч. – Киев: Вища школа, 1989; 1990. –350 с.

17. Подскребко М. Д., Томило С. С., Шинкевич А. Н. Задания по расчетно-графическим работам курса «Прикладная механика». Ч. 1. – Мн.: БИМСХ, 1990. – 59 с.

18. Пособие к решению задач по сопротивлению материалов: Учеб. пособие для техн. вузов/ И. М. Миролюбов, С. А. Енгалычев, Н. Д. Сергеевский и др., – 5-е изд., перераб. и доп. – М.: Высшая школа, 1985. – 399 с.

19. Прикладная механика. Методические указания и контрольные задания для студентов-заочников/ Под редакцией П. Г. Гузенкова. – М.: Машиностроение, 1982. – 112 с.

20. Прикладная механика: Учеб. пособие/ А.Т.Скойбеда, А.А.Миклашевич, Е.Н.Левковский и др.; Под общ. ред. А.Т.Скойбеды. – Мн.: Высшая школа, 1997. – 552 с.

21. Руденок Е. Н., Соколовская В. П. Техническая механика. Сб. заданий: Учеб. пособие. – Мн.: Высшая школа, 1990. – 238 с.

22. Сборник задач по сопротивлению материалов / Под ред. В.К.Качурина. – М.: Наука, 1970. – 432 с.

23. Сборник задач по технической механике / В.В. Багреёв, А.И. Винокуров, В. А. Киселёв т др. – Л.: Судостроение, 1968.

24. Соколов Б. Ф., Моношков А. Н., Шатруков В. И. Методические указания к семестровым заданиям по объединенному курсу «Теоретическая и прикладная механика». – Челябинск: Челябинский ин-т механизации и электрификации сельского хозяйства, 1985.

25. Феодосьев В. И. Сопротивление материалов. – М.: Наука, 1986. – 512 с.

26. Феодосьев В. И. Избранные задачи и вопросы по сопротивлению материалов. – 4-е изд., исп. и доп. – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1973. –400 с.

27. Шапиро Д. М., Подорванова А. И., Миронов А. Н. Сборник задач по сопротивлению материалов: Учеб. пособие для машиностроительных техникумов. – 3-е изд., переработ. – М.: Высшая школа, 1970.

28. Юдин В. А., Петрокас Л. В. Теория механизмов и машин. – М.: Машиностроение, 1977. – 527 с.

29. Яблонский А. А. Курс теоретической механи­ки. В 2 ч. Ч. 1. Статика, кинематика. – 7-е изд., стереотип. – СПб.: Лань, 1999.

[1] Размеры даны для колес с внешними зубьями.