Моделювання у теорії ІМ

У теорії ІМ більшу групу завдань вирішують на основі моделювання випадкових величин і випадкових дискретних подій (процесів). Моделювання випадкової величини (випадкового процесу) найчастіше здійснюється за допомогою так званого методу Монте-Карло, у якому застосовується ідея конструктивного імовірнісного простору й дії деякого випадкового механізму.

Конструктивний простір відповідає уявленню випадкової величини у вигляді кінцевої або рахункової послідовності незалежних величин, рівномірно розподілених на відрізку [0,1]. Послідовність чисел називається рівномірно розподіленою 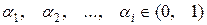, якщо для будь-якої інтегрувальної на відрізку [0,1] за Риманом функції має місце співвідношення

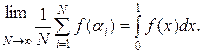
Завдання методу Монте-Карло полягає в одержанні за низкою реалізацій деяких відомостей про розподіл випадкової величини, тобто є, таким чином, типовим завданням математичної статистики.

Останні досягнення в області обчислювальної техніки породили новий напрямок у дослідженні складних процесів і систем — імітаційне моделювання. Воно дозволяє досліджувати як детерміновані, так і випадкові процеси й системи.

Імітаційне моделювання на ЕОМ викликало великий інтерес у дослідників, проектувальників і експлуатаційників технічних систем. При його використанні є можливим істотно заощадити час і витрати на одержання необхідних даних про властивості систем у порівнянні з використанням звичайних «традиційних» методів натурних випробувань або аналітичних досліджень. У зв'язку з появою потужних ЕОМ третього й наступного поколінь і розвитком спеціальних мов програмування ефективність імітаційного моделювання сильно зросла.