Деформационные свойства.

Деформацией называется свойство горных пород менять под нагрузкой форму сложения и объем. Она зависит от типа породы, от размеров нагрузки, от способов передачи нагрузки на породы. При применении внешнего усилия в породе возникает противодействующее внутреннее напряжение, его изучением занимается механика грунтов.

В условиях равновесия напряжения, возникающие в породе равны действию внешних усилий.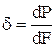

d - напряжение в породе, кГ/см²;

Р - внешняя нагрузка, кГ;

F - площадь приложения нагрузки, см².

Каждую внешнюю силу, действующую на произвольно выбранную площадку или сечение внутри породы, можно разложить на две силы – нормальную к площадке и касательную к ней (рис.6.1). Эти две силы, отнесенные к единице площади, называют, соответственно, нормальным или сжимающим d_n и касательным или сдвигающим t напряжением.

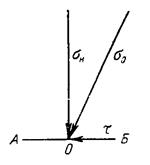
Рис. 6.1. Схема распределения напряжений в данной точке О элементарной площадки АБ в любом сечении породы:

σ₀ – общее напряжение; σ_Н – нормальное напряжение; τ – касательное напряжение.

Под действием нормальной силы развивается деформация сжатия (уменьшение расстояния между двумя параллельными площадками), под действием касательной - деформация сдвига (взаимное перемещение двух параллельных площадок относительно друг друга).

В каждой точки нагруженной породы можно выделить элементарный кубик, на взаимно перпендикулярные грани которого действуют нормальные напряжения. Эти нормальные напряжения называют главными напряжениями (σ₁, σ₂,_, σ₃).

При изучении внутренних напряжений пользуются в общем случае тремя схемами.

1. Одноосное напряженное состояние - усилие действует только по одной оси, действует только одно главное напряжение, а два других равны нулю. .

2. Двухосное напряженное состояние - на породу действуют 2 взаимно перпендикулярных напряжения.

3. Трехосное или объемное (всестороннее) напряженное состояние, когда на породу действуют три главных напряжения. Такое напряженное состояние характерно для горных пород в естественных условиях залегания, а также при работе под сооружениями.

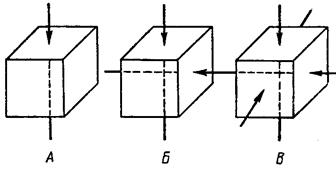
Рис. 6.2. Схемы напряженного состояния породы:

А- одноосное, Б- двухосное, В- трехосное.

Деформация горных пород возникают тогда, когда внешние силы, действующие на породу, становятся больше внутренних сил в породе (трение и сцепление), стремящихся сохранить целостность породы - форму и размер составляющих ее зерен и связи между ними. Все деформации возникают в наиболее неблагоприятных сечениях, в которых возникают и действуют максимальные нормальное и касательные напряжения.

Если внутренние силы породы равны напряжениям, вызванным внешними усилиями, то порода находится в предельном напряженном состоянии, предшествующим ее деформациям и разрушению.

Характер деформаций у пород с жесткими связями аналогичен характеру деформации твердых тел, которое описывается законом Гука:

d = е ^. Е

где d - напряжение, возникающее в породе под действием внешней нагрузки (кГ/см²),

е - относительная деформация;

Е - модуль упругости (характеристика породы) - кГ/см².

Модуль упругости равен напряжению, вызвавшему деформацию, равную единице.

Модуль упругости – основная характеристика деформационных свойств всех твердых тел, у которых деформации носят упругий характер. Под упругими деформациями понимают обратимые деформации, т.е. такие деформации, которые исчезают после снятия нагрузки, вызвавшей их.

В горных породах строго упругих деформаций не наблюдается. Для них характерны еще и остаточные – пластические деформации, поэтому, деформационные свойства горных пород, кроме модуля упругости (модуль Юнга) Е и коэффициента Пуассона μ, характеризуются коэффициентом бокового давления z и модулем общей деформации Е₀.

Возьмем образец скальной породы высотой l₁ и передадим на этот образец сжимающее усилие σ (кг/см²) – рис. 6.3. В результате сжатия высота образца уменьшается до l₂, а поперечные размеры увеличатся с d₁ до d₂. Разность l₁ – l₂=Δl называют абсолютной продольной деформацией, а d₂ – d₁ = Δ d – абсолютной поперечной деформацией.

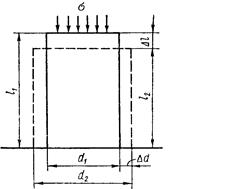
Рис. 6.3. Схема деформации горной породы при одноосном сжатии.

Далее определяются

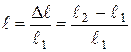- относительная продольная деформация;

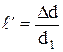- относительная поперечная деформация.

Отношение относительной поперечной к относительной продольной деформации называется коэффициентом Пуассона: .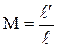

Чем больше значение коэффициента Пуассона, тем более порода може деформироваться. В твердых породах он изменяется от 0.1 до 0.4.

При действии на породу вертикальной нагрузки значительная часть ее - нормальная составляющая - вызывает деформацию в породе, а другая часть (тангенциальная составляющая) передается через породу в стороны, вызывая боковое давление. Численно эта часть нагрузки или боковое давление Р_б, равна вертикальной нагрузке, умноженной на коэффициент бокового давления z ,

Р_б = z ^. Р

где z - коэффициент бокового давления, показывающий, какая часть вертикальной нагрузки передается через породу в стороны и вызывает касательные напряжения.

z ¸ 0,0 - 0,1 - у крепких скальных пород;

z ¸ 0,2 - 0,3 - у полускальных пород.

Модуль общей упругости Е₀ характеризует деформации породы под нагрузкой – как упругие, так и остаточные деформации.

Исследования показали, что в породах с жесткими связями модуль упругости больше модуля общей деформации, причем Е₀ зависит от величины внешней нагрузки. Таким образом, для получения более достоверных данных его определение должно проводиться под нагрузками (нагрузками, рассчитанными под проектное сооружение).

Е₀ зависит от скорости приложения нагрузки. Различают статические и динамические определения показателей упругости пород.