Воздействие стоячих волн

Рассмотрим оградительное сооружение, расчетная схема которого показана на рисунке 2.116. Размеры волнолома и волновые нагрузки от стоячих волн взяты из [14] (пример 8.1, стр. 249) или из [15] (пример 1, стр. 14).

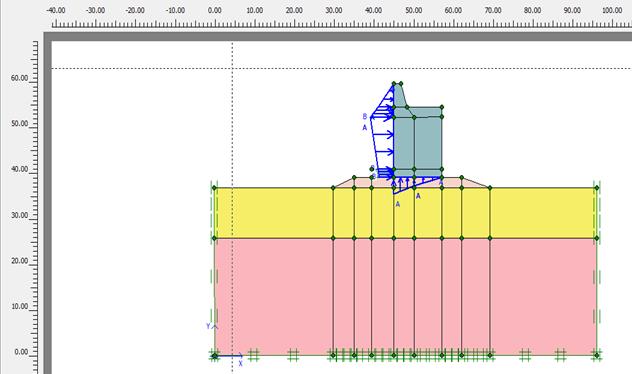
Рис. 2.116. Расчетная схема волнолома

Грунты массива состоят из двух слоев, имеющих следующие физико-механические свойства: сцепление с (в кН\м²), угол внутреннего трения φ (в градусах), модуль деформации Е (в кН\м²) и коэффициент Пуассона (безразмерная величина). Первый слой (песок) – с =6, φ = 38, Е = 49000, µ = 0,3; второй слой (суглинок) – с = 35, φ = 25, Е = 30000, µ = 0,33. Каменная постель имеет следующие характеристики: с = 16, φ = 45, Е = 60000, µ = 0,3. Считаем, что массивная стенка работает в упругой стадии. Глубина воды до верха сооружения равна 15 м, высота каменной постели составляет 2 м.

Расчет выполняется в три этапа. На первом этапе производится расчет только грунтового массива от действия его собственного веса, т. е. до начала строительства волнолома. На втором этапе перемещения, полученные на первом этапе, обнуляются, а напряжения сохраняются, и определяется напряженно-деформированное состояние системы после возведения каменной постели и стенки. На третьем этапе к стенке прикладывается волновая нагрузка при высоте волн 6 м и их длине 100 м. Расчетные характеристики взяты из указанного выше примера. Они показывают, что для данного случая допускается производить расчет от действия стоячих волн.

Ввод данных и порядок выполнения расчета в системе PLAXIS для этого примера аналогичны предыдущим, ранее рассмотренным примерам, поэтому они здесь не приводятся. На первом и втором этапах расчета, полученные данные показывают, что сооружение работает без повреждений. Например, его полные перемещения после второго этапа расчета, т. е. после постройки, приведены на рисунке 2.117. Здесь наибольшее перемещение стенки равно 4,7 см. Но на третьем этапе расчета, когда на стенку действует волновое давление, происходит разрушение сооружения. Так начало опрокидывания стенки показано красными стрелками на рисунке 2.118.

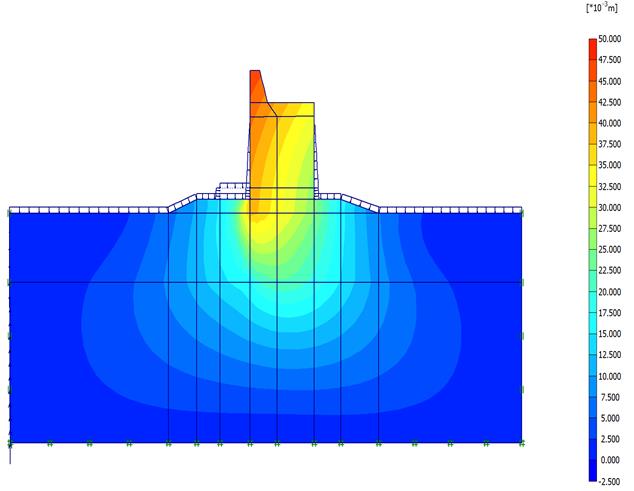Рис. 2.117. Эпюра полных перемещений волнолома после его сооружения

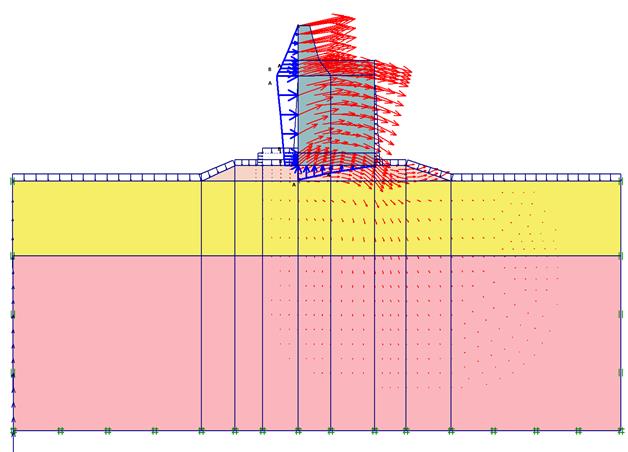
Рис. 2.118. Опрокидывание стенки от волнового воздействия

Приведенные результаты показывают, что оградительное сооружение необходимо рассматривать при разработке расчетной схемы и при выполнении расчета только как единую систему, состоящую из стенки, каменной постели и грунтового массива. Раздельный расчет без одновременного учета работы каменной постели и грунтового массива, как выполнено в [14], может привести к катастрофическим результатам.

Рассмотрим стенку волнолома более массивной формы, например, как показано на рисунке 2.119. Размеры можно определить по масштабным линейкам. Статический расчет этого оградительного сооружения выполняется также в три этапа. Рассмотрим результаты, полученные после третьего этапа, т. е. после воздействия стоячей волны на стенку. На рисунке 2.120 приведена эпюра полных перемещений системы. Наибольшее перемещение расположено под правым нижним углом стенки, оно равно 8,5 см. Эпюра полных напряжений изображена на рисунке 2.121. Наибольшее напряжение, равное 184,2 кН\м², находится в грунте также под правым нижним углом стенки. Схема образованных пластических зон, расположенных в постеле и грунтовом массиве, показана на рисунке 2.122. Они охватывают значительные области этих элементов системы.

Расчеты оградительных сооружений для других сочетаний волновых нагрузок, приведенных в работах [1, 14], выполняются в системе PLAXIS аналогично выше исследованным примерам, поэтому их не рассматриваем.

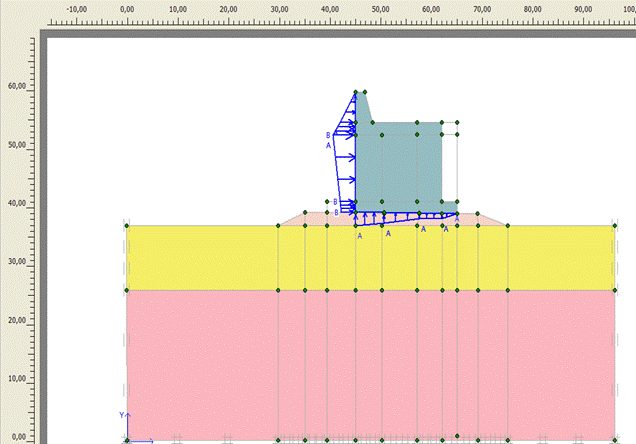
Рис. 2.119. Расчетная схема оградительного сооружения

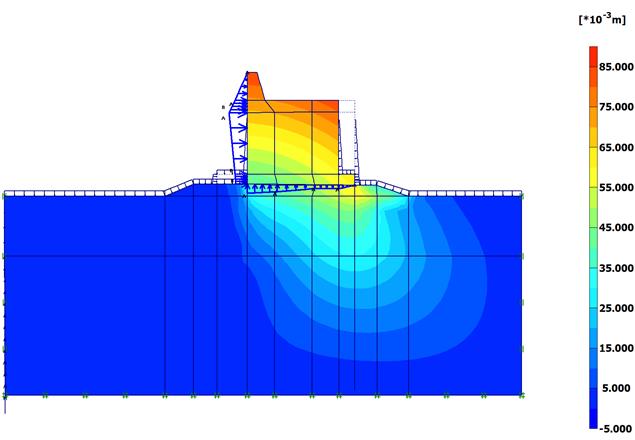
Рис. 2.120. Эпюра полных перемещений системы

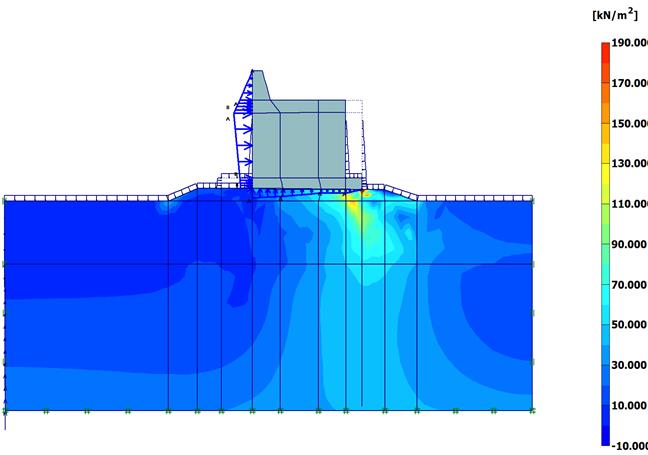
Рис. 2.121. Эпюра полных напряжений системы

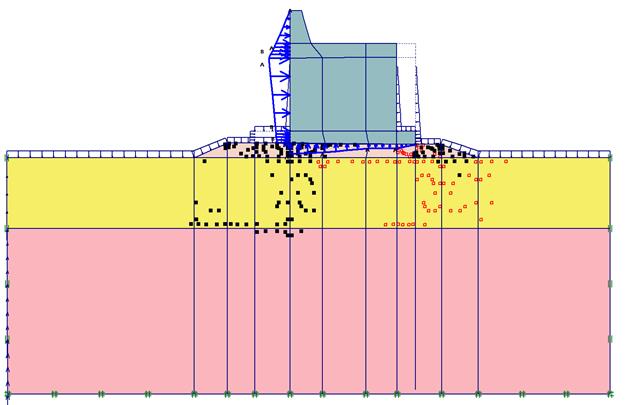
Рис. 2.122. Схема пластических зон в системе