Матрица поворота вокруг произвольной оси

В ряде случаев подвижная система координат OUVW может совершать поворот на угол j относительно произвольной оси r, представляющей собой единичный вектор с компонентами r_x, r_y и r_z, выходящие из начала координат О. Это применяется тогда, когда нужно упростить последовательность поворотов относительно основных осей систем координат OXYZ и/или OUVW. Их можно заменить одним поворотом системы OUVW вокруг оси r (рис. 3.1).

Чтобы получить матрицу поворотаR_r,j , можно сначала произвести ряд поворотов относительно осей системы OXYZ, чтобы совместить ось r с осью OZ. Затем произвести требуемый поворот вокруг оси r на угол j и опять ряд поворотов относительно системы OXYZ, возвращающих ось OZ в исходное положение.

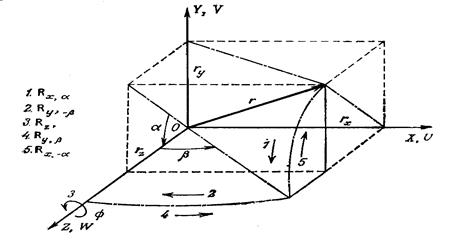
Рисунок 3.1. Вращение вокруг произвольной оси

Из рис. 3.1 видно, что совмещение осей OZ и rможет быть реализовано с помощью поворота на угол a относительно оси OX, тогда ось rв результате окажется в плоскости XZ, а затем на угол -b, вокруг оси OY, тогда в результате оси OZ и r совпадут. После поворота на угол j относительно OZ или r проведём прежнюю операцию в обратном порядке с обратными знаками. Результирующая матрица поворота равна:

R _r,j = R _x,-a ×R _y,b ×R_z,j ×R _y,-b ×R _x,a =

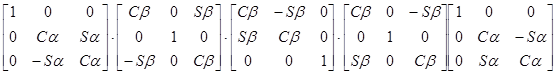
Из этого легко определить, что:

sina = 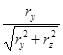; cosa = 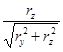; sinb = r_x; cosb = .

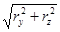Подстановка этих равенств в предыдущее выражение дает:

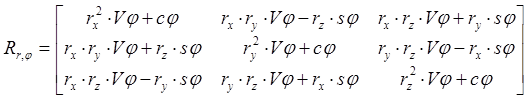, (3-1)

где Vj = vers j= 1– cosj.

Это очень полезная матрица поворота.