Формирование системы координат для манипулятора Пума
Шаг 1. Формирование базовой системы координат.
Сформировать правую ортонормированную систему координат (х0, y0, z0), связанную с основанием, ось z0 вдоль оси 1-го сочленения к «плечу» манипулятора. Оси х0 и y0 выбираются произвольно при условии их перпендикулярности оси z0.
Шаг 2. Начало и цикл. Для всех i ( i=1,2 … n-1) выполнить шаги 3-6.
Шаг 3. Формирование осей сочленения. Направить ось zi вдоль оси движения (вращательного или поступательного) i+1-го сочленения.
Шаг 4. Формирование начала i-й системы координат. Расположить начало i-й системы координат на пересечении осей zi и zi-1 или на пересечении общей нормали к осям zi и zi-1 с осью zi.
Шаг 5. Формирование оси xi. Выбрать единичный вектор xi следующим образом: xi = ±( zi-1 × zi)/ || zi-1 × zi || или вдоль общего перпендикуляра к осям zi-1 и zi, если они параллельны.
Шаг 6. Формирование оси yi Положить yi = +( zi × xi)/ ||zi ×xi|| , получив тем самым правостороннюю систему координат.
Шаг 7. Формирование системы координат схвата. Как правило, n-е сочленение является вращательным. Сформировать ось zn, направив ее вдоль оси zn-1 и от робота. Выбрать ось хn так, чтобы она была перпендикулярна осям zn-1 и zn.
Шаг 8. Определение параметров звеньев и сочленений. Для каждого i
(i =1…n) выполнить шаги 9-12.
Шаг 9. Определение di Расстояние di – от начала (i-1)-й системы координат до пересечения оси zi-1 с осью xi и началом i-й системы координат, отсчитываемой вдоль оси zi-1. Если i-е соединение – поступательное, то di – присоединенная переменная.
Шаг 10. Определение ai - расстояния между пересечением оси zi-1 с осью xi и началом i-й системы координат, отсчитываемой вдоль оси xi.
Шаг 11. Определение Qi – угла поворота оси xi -1 вокруг оси zi-1, чтобы она стала сонаправлена с осью xi. Если i -е сочленение – вращательное, то Qi-присоединенная переменная.
Шаг 12. Определение αi – угла поворота оси zi -1 вокруг оси xi, чтобы она стала сонаправлена с осью zi .
После построения ДХ-координат для всех звеньев можно построить однородные матрицы преобразования, связывающие i-ю и (i-1)-ю системы координат:
i-1Ai= Tz,dTz,QTx,aTx,α= 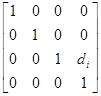
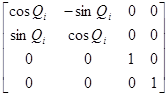
 ×
×
× 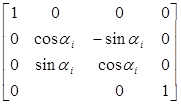 =
= 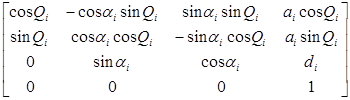 . (5-1)
. (5-1)
Преобразуя (3-1), найдем, что матрица, обратная к i-1Аi, имеет вид:
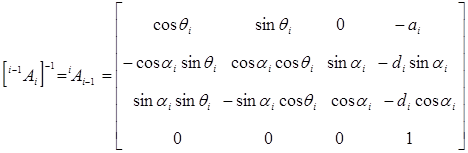 , (5-2)
, (5-2)
где 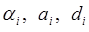 - константы, а
- константы, а 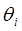 - присоединенная переменная, если рассматриваемое сочленение – вращательное.
- присоединенная переменная, если рассматриваемое сочленение – вращательное.
Используя матрицу 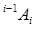 , можно связать однородные координаты рi точки р относительно i-й системы координат (точка р покоится в i–й системе координат)с односторонними координатами этой точки относительно (i-1)-й системы тсчета, связанной с (i-1)-м звеном. Эта связь устанавливается равенством:
, можно связать однородные координаты рi точки р относительно i-й системы координат (точка р покоится в i–й системе координат)с односторонними координатами этой точки относительно (i-1)-й системы тсчета, связанной с (i-1)-м звеном. Эта связь устанавливается равенством:
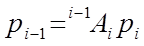 , (5-3)
, (5-3)
где 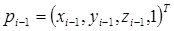 и
и 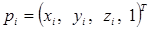 .
.
Для шестизвенного манипулятора Пума были определены шесть матриц 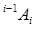 , соответствующие показанным на рис. 5.4. системам координат. Эти матрицы представлены ниже:
, соответствующие показанным на рис. 5.4. системам координат. Эти матрицы представлены ниже:
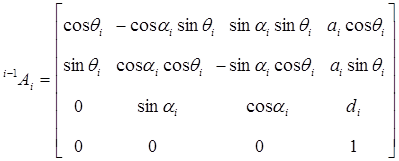 ,
,
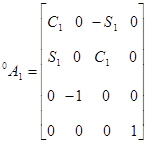 ,
, 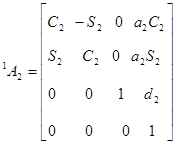 ,
,
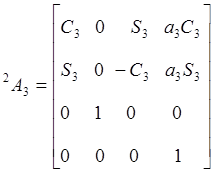 ,
, 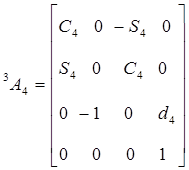
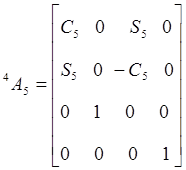 ,
, 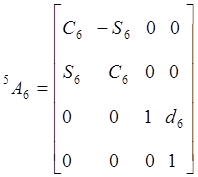 ,
,
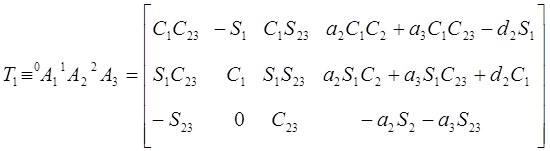 ,
,
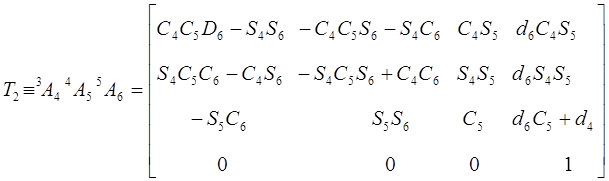 ,
,
где
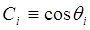 ;
; 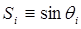 ;
; 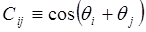 ;
; 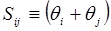 .
.
Дата добавления: 2021-11-16; просмотров: 704;











