Кинематика манипулятора

Предметом кинематики манипулятора является аналитическое описание геометрии движения манипулятора относительно некоторой заданной абсолютной системы координат без учёта сил и моментов, порождающих это движение. Таким образом, задачей кинематики является аналитическое описание пространственного расположения манипулятора в зависимости от времени и, в частности, установление связи между значениями присоединённых координат манипулятора и положением и ориентацией его схвата в декартовом пространстве.

Механический манипулятор можно рассматривать как разомкнутую цепь, которая состоит из нескольких твёрдых звеньев, последовательно соединенных вращательными или поступательными сочленениями, приводимых в движение силовыми приводами.

Основные задачи кинематики манипулятора:

1. Для конкретного манипулятора по известному вектору присоединённых углов (обобщённых координат q(t)=(q₁(t),q₂(t),...,q_n(t))^g) и заданным геометрическим параметром звеньев (n – число степеней свободы) определить положение и ориентацию схвата манипулятора относительно абсолютной системы координат.

2. При известных геометрических параметрах звеньев найти все возможные векторы присоединённых переменных манипулятора, обеспечивающие заданное положение и ориентацию схвата относительно абсолютной систем координат.

Первую из этих задач принято называть прямой, а вторую – обратной задачей кинематики манипулятора.

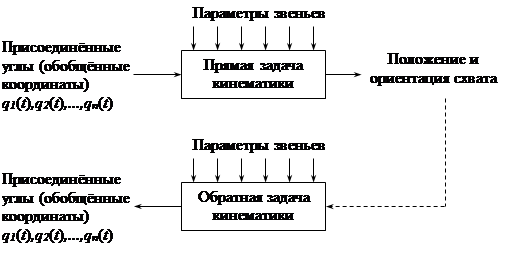
Рисунок 2.1. Схема взаимосвязи прямой и обратной задач кинематики

Для описания взаимного пространственного положения двух смежных звеньев используют однородную матрицу преобразования размерностью 4´4.