Синтез комбинационных схем

Синтез логического устройства выполняют на основе заданной каким-либо из известных способов логической функции (функции алгебры логики), описывающей логику функционирования устройства.

Наиболее наглядным способом представления логической функции является использование таблицы истинности. Поэтому воспользуемся этим способом при изложении методики синтеза комбинационной схемы.

В общем случае процедура синтеза комбинационной схемы состоит из следующих этапов:

а) уточнение алгоритма работы логического устройства;

б) составление таблицы истинности для логической функции, реализуемой логическим устройством;

в) составление СДНФ (СКНФ) логической функции;

г) минимизация СДНФ (СКНФ) логической функции;

д) разработка функциональной схемы логического устройства;

е) проверка правильности функционирования разработанного логического устройства.

Рассмотрим каждый из этапов более подробно.

В процессе уточнения алгоритма работы логического устройства необходимо установить, какие значения принимает каждая из k логических функций на всех наборах входных переменных x_i. На практике при синтезе логического устройства может оказаться, что по условиям работы устройства появление некоторых сочетаний входных переменных (наборов переменных) невозможно, поэтому значения логической функции на этих наборах не задаются, то есть функция определена не на всех 2^п наборах логических переменных, где п – число логических переменных (число входов синтезируемого логического устройства). Как отмечено ранее, наборы логических переменных, на которых функция не определена, принято называть запрещенными.

После уточнения алгоритма работы логического устройства составляется таблица истинности для логической функции (логических функций, если устройство имеет k выходов), реализуемой логическим устройством.

Предположим, что алгоритм функционирования логического устройства уже уточнен и представлен в виде таблицы истинности логической функции, показанной на рисунке 5.5. Как видно из рисунка, в таблице истинности в строках с запрещенными наборами логических переменных вместо значений функции 0 или 1 записан знак «*». В дальнейшем при минимизации логической функции методом Карно-Вейча в диаграмме Вейча этот знак может быть заменен значением «0» или «1». В частности, если для синтеза логического устройства предполагается использовать ДНФ функции, то записывают «1», а если КНФ – то «0».

Следующим этапом после заполнения таблицы истинности является составление логического выражения в виде СДНФ или СКНФ логической функции. В сущности, не имеет особого значения, какую нормальную форму логической функции использовать. От этого будет зависеть только то, на какой элементной базе будет реализовано логическое устройство.

Составим СДНФ логической функции у, заданной таблицей истинности (рисунок 5.5):

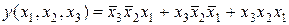. (5.7)

СКНФ логической функции у будет иметь вид:

. (5.8)

Логические выражения (5.7) и (5.8) могут быть использованы для синтеза функциональной схемы логического устройства. Оба выражения полностью определяют логическую функцию у(х₁, х₂, х₃), поэтому и синтезированные на их основе логические устройства будут функционировать в соответствии с алгоритмом, описанным таблицей истинности логической функции (рисунок 5.5). Основное отличие в двух полученных функциональных схемах будет состоять в элементной базе, на которой реализованы устройства. В качестве примера на рисунке 5.21 приведена схема логического устройства, синтезированная на основе выражения (5.7), а на рисунке 5.22 – синтезированная на основе выражения (5.8).

Из рисунков видно, что полученные схемы отличаются не только элементной базой, но и сложностью построения (количеством элементов).

Рисунок 5.21 – Комбинационная схема, синтезированная на основе СДНФ

логической функции

Рисунок 5.22 – Комбинационная схема, синтезированная на основе СКНФ

логической функции

При практической реализации схемы на интегральных микросхемах, например, транзисторно-транзисторной логики (ТТЛ), ее конфигурация может измениться. Это связано с тем, что многовходовые логические элементы приходится заменять несколькими элементами с меньшим числом входов (на основе сочетательных законов алгебры логики для дизъюнкции или конъюнкции нескольких переменных). В частности, интегральные микросхемы ТТЛ серий 155, 555 и др. содержат только двухвходовые логические элементы И (например ИМС К155ЛИ1) и ИЛИ (ИМС К155ЛЕ1). Следовательно, каждый трехвходовый логический элемент в рассматриваемых схемах должен быть заменен двумя двухвходовыми элементами.

После того, как получена схема логического устройства, необходимо убедиться (подстановкой значений логических переменных), что на всех разрешенных наборах логических переменных значение логической функции на выходе устройства равно соответствующему значению логической функции, заданному в таблице истинности.

Ранее было показано, что логическое устройство, синтезированное на основе СДНФ или СКНФ по количеству логических элементов и числу входов этих элементов, как правило, бывает не оптимальным. С целью оптимизации схемы логического устройства необходимо выполнить минимизацию логической функции.

Воспользуемся методом Карно-Вейча и получим минимальную форму логической функции для рассматриваемого примера. Поскольку диаграмма Вейча (карта Карно) является упрощенной формой записи таблицы истинности, то к минимизации можно перейти непосредственно после заполнения таблицы истинности, минуя этап составления СДНФ (СКНФ) логической функции.

В подразделе 5.4 уже выполнена минимизация рассматриваемой функции, поэтому используем ранее полученные выражения в виде ДНФ (5.3) и КНФ (5.4) логической функции и синтезируем функциональные схемы логического устройства. Схема устройства, реализованного на основе выражения (5.3), представлена на рисунке 5.23, а устройства, реализованного на основе выражения (5.4) – на рисунке 5.24.

Рисунок 5.23 – Комбинационная схема, синтезированная на основе

ДНФ минимизированной логической функции

Рисунок 5.24 – Комбинационная схема, синтезированная на основе

КНФ минимизированной логической функции

Из сравнения рисунков 5.21 и 5.23, а также рисунков 5.22 и 5.24 видно, что после минимизации логической функции структура логического устройства существенно упрощается. Функциональные схемы логического устройства содержат меньшее число логических элементов с меньшим числом входов у этих элементов. Для завершения решения задачи синтеза следует, как отмечено ранее, убедиться, что на всех наборах логических переменных, на которых определена логическая функция, значение логической функции на выходе устройства равно соответствующему значению логической функции, заданному в таблице истинности.