Достаточные условия сходимости метода простой итерации (теоремы, оценки погрешностей).

Теорема сходимости:

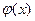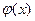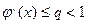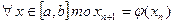Пусть существует функция определена и дифференцируема на отрезке [a,b]. Причем все значения функции принадлежат отрезку [a,b], тогда если существует правильная дробь 0<q<1 такая что для где n=0,1,2… сходятся независимо от начального приближения 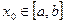, причем предельное значение 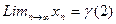и этот корень единственный.

Доказательство:

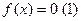приводя к эквивалентному виду

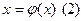
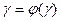
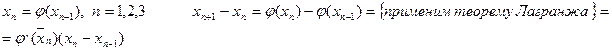
Обозначим за q=sup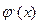

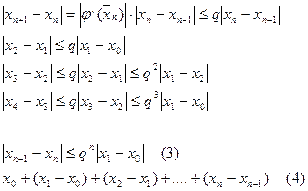
Последовательность приближений х_n есть частичные суммы S_n+1 ряда 4

S₂=x₁

S₃=x₂……

S_n+1=x_n

Члены ряда 4 по абсолютной величине начиная с 3, меньше членов арифметической прогрессии со значениями 0<q<1, q;q²;q³;…;qⁿ.

Геометрическая прогрессия является сходящейся, значит существует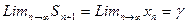

В силу непрерывности 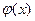можно записать 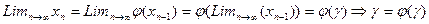, значит этот корень уравнения (2).

Докажем единственность:

Пусть существует 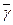которая является корнем (2)

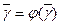, найдем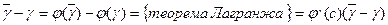

с- внутренняя точка отрезка [a,b].

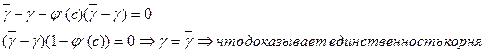
Замечание 1:

1. Константа q – носит название константы Липшиця.

2. Наша теорема справедлива, если функция 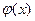будет определена и дифференцируема на интервале (- 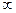, + 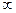), но лишь в том случае, когда константа Липшиця .

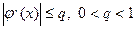3. В условиях теоремы метод итерации сходится для любого х₀ 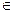[a,b] благодаря чему он является самоисправляющийся, т.е. отдельные ошибки в вычислениях не влияют на результат.

Оценка приближений

Рассмотрим модуль разности 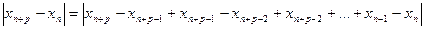известно, что модуль суммы 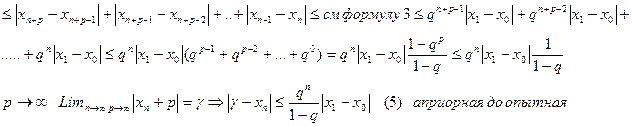Процесс итерации сходится тем быстрее чем меньше q.

При желании можно вывести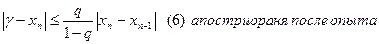

Замечание: Если q=1\2, то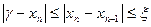

Процесс итерации следует продолжать до тех пор пока 2 последующих приближений не будет удовлетворять условию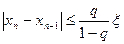

Докажем, что каждое из приближений x_n располагается ближе к корню.

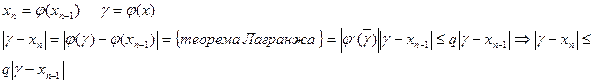
т.е. последовательность приближений изменяется монотонно и каждое последующее приближение n 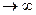располагается ближе к корню .

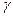Теорема сходимости 2:

Пусть 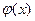определена и дифференцируема на некотором отрезке [a,b], причем х= 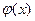имеет корень 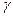лежащий в более узком отрезк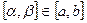е , где 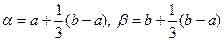тогда если:

1.

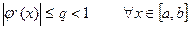
2. 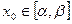, то все последующие приближения будут принадлежать интервалу [a,b], и процесс итерации будет сходится к единственному корню уравнения х= 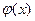, причем будет выполняться оценка (5).