Метод Эйлера для систем дифференциальных уравнений.

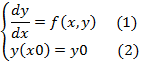
Выбрав достаточно малый шаг h построим систему равностоящих точек

Xi=x+ih (io=1,2,…) {xi=xi-1 + h}

Что бы решить задачу Коши 1 и 2 нужно найти интегрированную кривую, которая проходит через точку М0(х0,у0). В методе Эйлера искомую кривую заменяют ломанной MiMi+1 – прямолинейные отрезки расположены между прямыми x=xi; x=xi+1, причем эти отрезки имеют наклон, который равен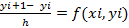

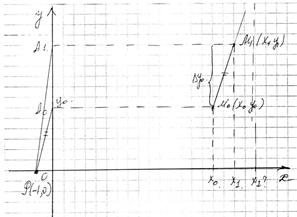
Угловой коэффициент 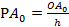через М0 проводим отрезок = 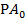, через М1 проводим отрезок = 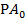и параллельно проводим отрезок = 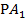отсюда следует М2(х2,у2) построим ломанную , которая проходит через начальную точку и yi+1= yi+ 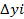; 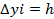*f(xi,yi)=h*yi’

Метод Эйлера явл простейшим численным методом интегрирования дифференциального уравнения.

Недостатком этого метода является

1. Малая точность

2. Систематическое накопление ошибок

Можно доказать что если правая часть F(x,y) (1) непрерывна , то последовательность ломанных Эйлера при h->0 на достаточно малом отрезке например [x0,x0+h ] будет стремиться к искомой интегральной кривой у=у(х). Этот метод легко распространяется на систему ДУ.

Пример: пусть дана задача Коши

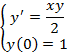
Отрезок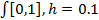

i-номер итеррации

х-аргумент

у-ф-ция

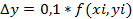
Аналог.Решение y=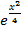

Метод Эйлера обладает малой точностью и дает удовлетворительный результат лишь при малых значениях h, это понятно, т.к по существу находя последующее значение интегральной ф-ции двумя членами ряда Тейлора на каждом частичном [xi,xi+1]

Yi+1=yi+hyi’ мы получаем погрешность порядка 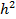. Кроме того при вычислении на следующем отрезке исходные данные не явл точными, поэтому есть смысл рассмотреть модификацию метода Эйлера.