Геометрия масс. Центр масс

При рассмотрении движения твердых тел и механических систем важное значение имеет точка, называемая центром масс. Техника вычисления центра масс, как и моментов инерции, относится к области курсов математики; там подобные задачи служат хорошими примерами по интегральному исчислению. Напомним основные положения.

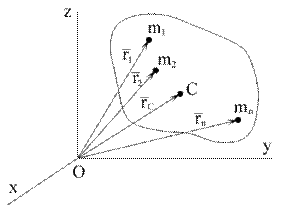Рис. 2.1

Если механическая система состоит из конечного числа материальных точек N с массами 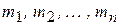, радиус-векторы которых проведены из одной и той же точки О – 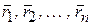(рис. 2.1), то центром масс называется геометрическая точка С, радиус-вектор которой 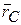определяется выражением

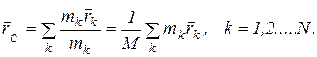, (2.1)

где 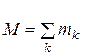- масса всей системы. Обозначая декартовы координаты материальных точек 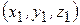, 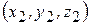… 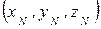, из (2.1) проецированием на декартовы оси координат получим следующие формулы для координат центра масс:

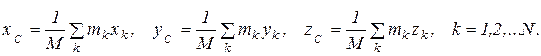(2.2)

Если механическая система представляет собой твердое тело, то формулы (2.1) и (2.2) принимают вид

,

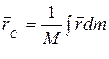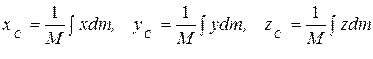, (2.3)

где 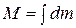– масса тела. Интегрирование ведется по всему объему тела.

Для плоского тела в формулах (2.2) и (2.3) 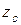=0, dm=rdA, A – площадь тела, интегрирование ведется по площади.