U-критерий Манна-Уитни
Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n1, n2 ≥ 3 или n1 = 2, n2 ≥ 5, и является более мощным, чем критерии Розенбаума.
Существует несколько способов использования критерия и несколько вариантов таблиц критических значений, соответствующих этим способам.
Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами. Мы помним, что 1-м рядом (выборкой, группой) мы называем тот ряд значений, в котором значения, по предварительной оценке, выше, а 2-м рядом – тот, где они предположительно ниже.
Чем меньше область перекрещивающихся значений, тем более вероятно, что различия достоверны. Иногда эти различия называют различиями в расположении двух выборок.
Эмпирическое значение критерия U отражает то, насколько велика зона совпадения между рядами. Поэтому чем меньше Uэмп, тем более вероятно, что различия достоверны.
Гипотезы
Н0: Уровень признака в группе 2 не ниже уровня признака в группе 1.
Н1: Уровень признака в группе 2 ниже уровня признака в группе 1.
Ограничения критерия U
1. В каждой выборке должно быть не менее 3 наблюдений: n1, n2 ≥ 3; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.
2. В каждой выборке должно быть не более 60 наблюдении; n1, n2 ≤ 60. Однако уже при n1, n2 > 20 ранжирование становиться достаточно трудоемким.
На наш взгляд, в случае, если n1, n2 > 20, лучше использовать другой критерий, а именно угловое преобразование Фишера в комбинации с критерием λ, позволяющим выявить критическую точку, в которой накапливаются максимальные различия между двумя сопоставляемыми выборками. Формулировка звучит сложно, но сам метод достаточно прост. Каждому исследователю лучше попробовать разные пути и выбрать тот, который кажется ему более подходящим.
Пример.Вернемся к результатам обследования студентов физического и психологического факультетов Ленинградского университета с помощью методики Д. Векслера для измерения вербального и невербального интеллекта. С помощью критерия Q Розенбаума мы в предыдущем параграфе смогли с высоким уровнем значимости определить, что уровень вербального интеллекта в выборке студентов физического факультета выше. Попытаемся установить теперь, воспроизводится ли этот результат при сопоставлении выборок по уровню невербального интеллекта. Данные приведены в таблице 11.3.
Можно ли утверждать, что одна из выборок превосходит другую по уровню невербального интеллекта?
Таблица 11.3
Индивидуальные значения невербального интеллекта в выборках студентов физического (n1 = 14) и психологического (n2 = 12) факультетов
| Студенты-физики | Студенты-психологи | ||||
| № п/п | Код имени испытуемого | Показатель невербального интеллекта | № п/п | Код имени испытуемого | Показатель невербального интеллекта |
| И.А. | Н.Т. | ||||
| К.А. | О.В. | ||||
| К.Е. | Е.В. | ||||
| П.А. | Ф.0. | ||||
| C.A. | И.Н. | ||||
| Ct.a. | И.Ч. |
Окончание табл. 11.3
| T.A. | И.В. | ||||
| Ф.А. | K.0. | ||||
| Ч.И. | P.P. | ||||
| Ц.А. | Р.И. | ||||
| Cm.a. | O.K. | ||||
| К.Ан. | H.K | ||||
| Б.Л. | |||||
| Ф.В. |
Критерий U требует тщательности и внимания. Прежде всего, необходимо помнить правила ранжирования.
При подсчете критерия U легче всего сразу приучить себя действовать по строгому алгоритму.
АЛГОРИТМ
Подсчета критерия U Манна-Унтни
1. Перенести все данные испытуемых на индивидуальные карточки.
2. Пометить карточки испытуемых выборки 1 одним цветом, скажем красным, а все карточки из выборки 2 – другим, например, синим.
3. Разложить все карточки в единый ряд по степени нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы мы работали с одной большой выборкой.
4. Проранжировать значения на карточках, приписывая меньшему значению меньший ранг. Всего рангов получится столько, сколько у нас (n1 + n2).
5. Вновь разложить карточки на две группы, ориентируясь на цветные обозначения: красные карточки в один ряд, синие – в другой.
6. Подсчитать сумму рангов отдельно на красных карточках (выборка 1) и на синих карточках (выборка 2). Проверить, совпадает ли общая сумма рангов с расчетной.
7. Определить большую из двух ранговых сумм.
8. Определить значение U по формуле:
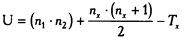 ,
,
где n1 – количество испытуемых в выборке 1;
n2 – количество испытуемых в выборке 2;
Тх – большая из двух ранговых сумм;
nх – количество испытуемых в группе с большей суммой рангов.
9. Определить критические значения U по таблице 8 приложения 1. Если Uэмп > Uкр.0,05, Н0 принимается. Если Uэмп ≤ Uкр.0,05, Н0 отвергается. Чем меньше значения U, тем достоверность различий выше.
Теперь проделаем всю эту работу на материале данного примера. В результате работы по 1-6 шагам алгоритма построим таблицу 11.4.
Таблица 11.4
Дата добавления: 2021-11-16; просмотров: 812;











