Математическое ожидание случайной величины и ее свойства.

Математическим ожиданием (МО) случайной величины называют ее среднее значение, определяемое по следующим формулам.

Для случайных дискретных величин МО равно

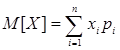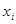, где - частное значение случайной дискретной величины; 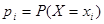- вероятность ее появления.

Для случайной непрерывной величины МО определяется выражением

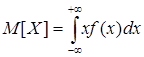, где x – частное значение случайной непрерывной величины; f(x)dx – элемент вероятности.

Математическое ожидание случайной величины представляет собой центр, около которого группируются частные значения ее.

Свойства математического ожидания:

а) математическое ожидание случайной величины может быть положительным и отрицательным, целым и дробным, и обладает размерностью случайной величины;

б) не все случайные величины имеют МО. Случайные величины не имеют МО, ес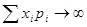ли или ;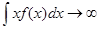

в) математическое ожидание постоянной величины равно самой постоянной величине, т.е. .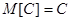

г) постоянную величину можно выносить за знак математического ожидания, т.е.

.

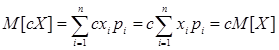Частный случай математического ожидания. Пусть случайная величина X может принимать только два частных значения 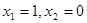. Тогда вероятности появления этих частных значений будут равны

.

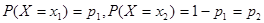Откуда математическое ожидание .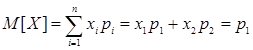

Следовательно, математическое ожидание такой случайной величины равна вероятности того, что случайная величина примет значение равное единице.

Пример 1: В технической системе имеется n элементов. Вероятность выхода из строя элемента в течении N часов работы равна p. Требуется определить математическое ожидание числа отказавших элементов в течении N часов работы.

Решение.

Обозначим через X – случайную величину числа отказавших элементов, а через M[X] - математическое ожидание этого числа.

Для использования формулы математического ожидания определяем из условия задачи, что случайная величина X принимает частные значения 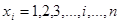, причем .

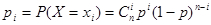Тогда математическое ожидание числа отказавших элементов будет равно

.

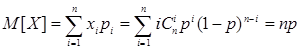Отсюда следует, что если случайная величина X подчиняется биномиальному закону, то ее МО равно произведению числа опытов на вероятность появления события в одном опыте.