Математическое описание линейных систем автоматического управления.
Порядок исследования САУ включает математическое описание системы, исследование ее установившихся режимов и исследование переходных режимов.
Математическое описание системы, т.е. получение ее математической модели, начинается с разбиения ее на звенья и описания этих звеньев. Это описание может осуществляться либо аналитически в виде уравнений, связывающих входные и выходные величины звена, либо графически в виде характеристик, описывающих ту же связь. По уравнениям или характеристикам отдельных звеньев составляются уравнения или характеристики системы в целом, на основании которых и исследуется система.
На прошлой лекции было дано понятие о функциональной схеме САУ (Рис. 2).
В функциональной схеме система разбита на звенья исходя из выполняемых ими функций, т.е. назначения. Для математического описания систему разбивают на звенья по другому принципу, а именно – исходя из удобства получения этого описания. Для этого систему следует разбивать на возможно более простые («мелкие») звенья, но вместе с тем необходимо, чтобы они обладали направленностью действия.
Звеном направленного действия называется звено, передающее воздействие только в одном направлении – с входа на выход, так что изменение состояния такого звена не влияет на состояние предшествующего звена, работающего на его вход. В результате при разбиении системы на звенья направленного действия математическое описание каждого такого звена может быть составлено без учета связей его с другими звеньями. Соответственно, математическое описание всей системы в целом может быть получено как совокупность составленных независимо друг от друга уравнений или характеристик отдельных звеньев, образующих систему, дополненных уравнениями связи между звеньями.
В результате разбиения САУ на звенья направленного действия и получения математического описания звеньев составляется структурная схема системы, которая и является ее математической моделью. Структурная схема системы состоит из прямоугольников, изображающих звенья схемы, и стрелок, соединяющих выходы и входы звеньев согласно связям между звеньями в системе. Стрелками показываются также внешние воздействия, приложенные к отдельным звеньям системы. Каждому звену структурной схемы придается описывающее его уравнение или характеристика. При этом уравнение обычно записывается прямо на схеме внутри изображающего звено прямоугольника в виде передаточной функции. Получение структурной схемы является конечной целью математического описания системы.
В качестве примера на рис. 2.1 показано разбиение на звенья системы автоматического регулирования напряжения синхронного генератора, которая была дана на прошлой лекции (Рис. 5), т.е. замкнутая система управления по отклонению. При этом принято, что усилитель регулятора состоит из двух частей: усилителя напряжения УН и усилителя мощности УМ в виде, например, электромашинного усилителя. Каждый из этих усилителей обладает направленностью действия и поэтому может быть выделен в виде отдельного звена.
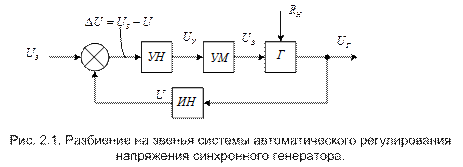
На рис.2.1 стрелками показаны внешние воздействия – задающее воздействие  и возмущение в виде сопротивления нагрузки на зажимах генератора. На этом же рисунке в виде кружочка, разделенного на секторы, дано условное изображение элемента сравнения, т.е. суммирующего элемента, выявляющего разность ΔU=UЗ – U. Рядом показаны знаки сигналов (плюс у UЗ и минус у U). Часто сектор, соответствующий вычитаемому сигналу, чернится, как показано на рис. 2.1.
и возмущение в виде сопротивления нагрузки на зажимах генератора. На этом же рисунке в виде кружочка, разделенного на секторы, дано условное изображение элемента сравнения, т.е. суммирующего элемента, выявляющего разность ΔU=UЗ – U. Рядом показаны знаки сигналов (плюс у UЗ и минус у U). Часто сектор, соответствующий вычитаемому сигналу, чернится, как показано на рис. 2.1.
Основная сложность, которая существует при выводе уравнений звеньев системы, заключается в необходимости установления допустимой степени идеализации и упрощения звеньев. Главным упрощением, к которому следует стремиться при выводе уравнений звеньев системы, является их линеаризация, т.е. описание линейными дифференциальными уравнениями. Линеаризация нелинейности, содержащейся в уравнении звена, заключается в замене этой нелинейности приближенной линейной зависимостью.
Мы не будем подробно останавливаться на математическом аспекте процедуры линеаризации. В двух словах можно сказать, что процедура линеаризации заключается в замене нелинейного дифференциального уравнения приближенным линейным. Понятно, что такую замену невозможно с достаточной степенью точности осуществить во всей области определения входных и выходных величин. Поэтому область линеаризации ограничивают вблизи некоторого номинального режима. Выбор такого номинального режима является, в общем случае, нетривиальной задачей. На практике чаще всего в качестве такого номинального режима выбирают установившийся режим, т.е. режим функционирования системы при времени, стремящемся к бесконечности (t®¥). Установивщийся режим, как мы знаем, характеризуется установившимися значениями выходной и входной величин – y0 и x0, соответсвенно.
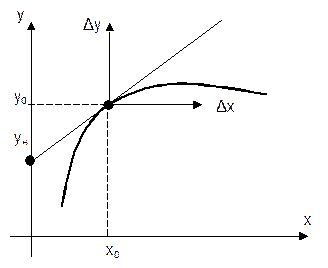
Рис. 2.2. Геометрическая интерпретация линеаризации.
Дадим геометрическую интерпретацию линеаризации. Изобразим графически нелинейную зависимость. Текущие значения координат y и x запишем как:
| y(t) = y0 + Dy(t); x(t) = x0 + Dx(t). | , где x(t), y(t) | – текущие значения, |
| y0, x0 | – установившиеся значения, | |
| Dy(t), Dx(t) | – отклонения от установившихся значений. |
В точке (x0, y0), определяемой установившимися значениями, заменим участок кривой касательной и получим прямую, описываемую линейным уравнением:
| y = yн + kx | , где yн | – постоянная величина; |
| k = [dy(t)/dx(t)]0 | – коэффициент, определяемый наклоном касательной к кривой в точке (x0, y0). |
Для исключения из уравнения величины yн перенесем начало координат в точку (x0, y0). Тогда получим линейное уравнение, связывающее между собой отклонения переменных величин от своих установившихся значений, вида:
Dy(t) = k Dx(t).
Таким образом, линеаризация уравнения геометрически может трактоваться как замена первоначальной кривой на касательную к ней прямую в точке установившегося режима. Очевидно, что эта замена тем точнее, чем меньше величины отклонений координат элемента от своих установившихся значений в исследуемом динамическом процессе.
Рассмотрим звено, описываемое нелинейной статической зависимостью Y=φ(X).

Пусть установившийся режим звена соответствует значениям входной и выходной величин X0 и Y0 (рис.2.2) и отклонения Х от Х0 в процессе работы звена достаточно малы. В этом случае исходную нелинейную зависимость Y=φ(X) можно разложить в ряд Тейлора в окрестностях точки установившегося режима и, отбросив члены ряда выше первого порядка малости, получить следующую приближенную зависимость:
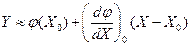 ,
,
где 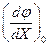 - значение производной функции φ(Х) по Х при подстановке в выражение этой производной Х=Х0.
- значение производной функции φ(Х) по Х при подстановке в выражение этой производной Х=Х0.
Это уравнение можно переписать в таком окончательном виде:
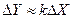 ,
,
где
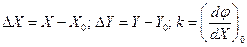 .
.
Таким образом, линеаризация уравнения геометрически может трактоваться как замена первоначальной кривой на касательную к ней прямую в точке установившегося режима. Очевидно, что эта замена тем точнее, чем меньше величины отклонений координат элемента от своих установившихся значений в исследуемом динамическом процессе.
Коэффициент k в уравнении равен тангенсу угла наклона этой касательной относительно оси абсцисс. Поэтому его величина может быть найдена чисто графическим построением без нахождения аналитического выражения для исходной нелинейной зависимости φ(Х), как было показано ранее.
Рассмотрим теперь более общий случай, когда звено описывается нелинейным уравнением, включающим производные по времени от входной и выходной величин:
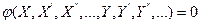 .
.
Такое уравнение называется динамическим. Оно характеризует переходный процесс, который протекает в системе.
Разложив, как и прежде, нелинейную функцию, находящуюся в левой части уравнения, в ряд Тейлора в точке установившегося режима, получим следующее линейное дифференциальное уравнение для приращений переменных:
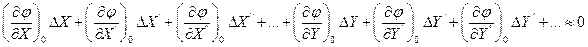 . (2.1)
. (2.1)
Здесь 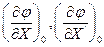 и т.д. – значения производных функции φ, получающиеся при подстановке значений Х0, Y0 и нулевых значений производных, соответствующих установившемуся режиму.
и т.д. – значения производных функции φ, получающиеся при подстановке значений Х0, Y0 и нулевых значений производных, соответствующих установившемуся режиму.
Показанная процедура линеаризации нелинейных звеньев приводит к приближенному описанию их линейными дифференциальными уравнениями в отклонениях.
В ТАУ приняты определенные формы записи линеаризованных дифференциальных уравнений звеньев. При этом уравнение (2.1) (с учетом только приведенных там членов) должно записываться так:
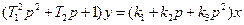 . (2.2)
. (2.2)
Здесь 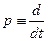 - оператор дифференцирования по времени;
- оператор дифференцирования по времени;
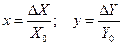 - приращения переменных в относительных единицах;
- приращения переменных в относительных единицах;
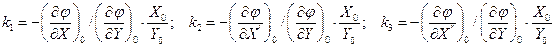 - коэффициенты передачи;
- коэффициенты передачи;
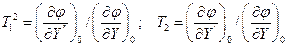 - постоянные времени.
- постоянные времени.
Особенности приведенной формы записи заключаются в следующем. Выходная величина и ее производные находятся в левой части уравнения, а входная величина и ее производные – в правой. Коэффициент при приращении выходной величины равен единице [в результате деления обеих частей уравнения на 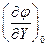 ].
].
Коэффициенты левой части уравнения – постоянные времени. Размерность их – секунда в степени, равной порядку производной, перед которой стоит данный коэффициент.
Другой формой записи линейных уравнений звеньев является запись с помощью передаточной функции. Уравнение (2.2) при этом принимает вид:
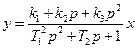 ,
,
или
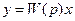 ,
,
где
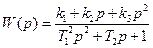 . (2.3)
. (2.3)
Дробь W(p) называется передаточной функцией звена. Пока будем рассматривать ее просто как удобный способ записи дифференциальных уравнений. Полное определение передаточной функции дам дальше, когда будем рассматривать преобразование Лапласа.
Рассматривая выше формы записи уравнений, принятые в ТАУ, мы оперировали для определенности уравнением 2-го порядка с одной входной величиной х. Однако в результате линеаризации реальных звеньев могут быть получены уравнения любого порядка. В общем случае звено САУ, имеющее n входов, описывается дифференциальным уравнением
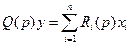 , (2.3,а)
, (2.3,а)
или в другом виде
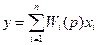 .
.
Здесь xi – входные воздействия на звено (i = 1,2,…,n); Q(p) и Ri(p) – полиномы относительно р; 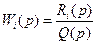 - передаточная функция звена для i – го входного воздействия.
- передаточная функция звена для i – го входного воздействия.
Дата добавления: 2018-05-10; просмотров: 2012;











