Применение преобразования Лапласа для решения линейных дифференциальных уравнений.

123

Линейные дифференциальные уравнения динамических систем решаются методами, которые подробно рассматриваются в курсах высшей математики. Для задач ТАУ наиболее удобным является операционный метод решения, основанный на функциональном преобразовании Лапласа

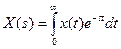Эта функция устанавливает соответствие между функцией времени х(t) (вещественной переменной) и функцией Х(s) (комплексной переменной s=c+jω). Здесь х(t) – оригинал, Х(s) – изображение. Символически эта операция записывается так:

Х(s) = .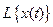

Чтобы вернуться от изображения к оригиналу, нужно выполнить обратное преобразование Лапласа по формуле:

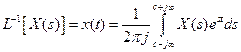Символ L указывает на то, что над функцией х(t) совершено преобразование Лапласа. На практике, чтобы не вычислять интегралы, для нахождения изображения по известному оригиналу или наоборот, используют специальные таблицы. Ниже приведено преобразование Лапласа для основных функций, которые наиболее часто встречаются при анализе систем автоматического управления.

Таблица преобразований Лапласа

х(t) (t > 0)	Х(s) = L[х(t)]
1(t)	1/s
δ(t)
t	1/s²
tⁿ	n!/sⁿ⁺¹
e^at	1/(s – a)
e^-at	1/(s + a)
t·e^at	1/(s – a)²
tⁿ·e^at	n!/(s – a)ⁿ⁺¹
sin(ωt)	ω/(s² + ω²)
cos(ωt)	s/(s² + ω²)
sin(ωt + φ)	[sin(φ) ·s + cos(φ) ·ω]/(s² + ω²)
cos(ωt + φ)	[cos(φ) ·s – sin(φ) ·ω]/(s² + ω²)
e^at·sin(ωt)	ω/[(s – a)² + ω²]
e^at·cos(ωt)	(s – a)/[(s – a)² + ω²]
e^at·sin(ωt + φ)	[sin(φ) ·(s – a) + cos(φ) ·ω]/[(s – a)² + ω²]
e^at·cos(ωt + φ)	[cos(φ) ·(s – a) – sin(φ) ·ω]/[(s – a)² + ω²]

(n! – выражение факториала, оно равно: n! = 1·2·3·4·…· (n – 1) ·n).

Особо следует отметить, что вид оригинала функций, приведенных в таблице, определен только для t > 0, т.е. значения переменной t ограничены областью положительных значений. Для отрицательных t значение функции х(t) равно нулю. Это важно, и игнорирование этого факта может на практике привести к существенным ошибкам.

Рассмотрев преобразование Лапласа, дадим определение передаточной функции звена САУ.

Передаточной функцией звена W(s) называется отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях, т.е.

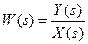. (2.4)

Для рассмотренного выше примера (выражение 2.3) передаточная функция W(s) будет отличаться от W(р) только заменой оператора дифференцирования р на комплексную переменную s и будет выглядеть следующим образом:

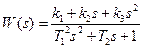. (2.5)

Динамическиехарактеристикиэлементов САУ.

Выше мы получили выражение (2.4), определяющее передаточную функцию линейного элемента системы управления. Это чрезвычайно важное выражение в теории автоматического управления. Оно связывает изображение выходного сигнала Y(s) c изображением входного сигнала Х(s) через динамические свойства элемента системы управления.

Ясно, что входное воздействие может иметь произвольный вид. Однако, чтобы охарактеризовать наиболее существенные черты динамического поведения объекта управления можно использовать некоторые "стандартные" виды входных воздействий. При этом выходной сигнал будет содержать определенную информацию о свойствах объекта управления.

Такие "стандартные" виды воздействий называются типовыми входными воздействиями. К ним относятся:

1) Единичная ступенчатая функция: 1(t).

2) Единичная импульсная функция: δ(t).

3) Гармонические функции: sin(ωt) и cos(ωt).

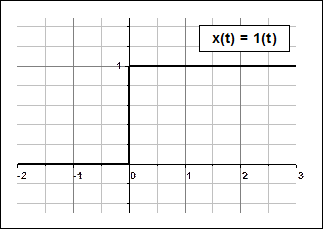
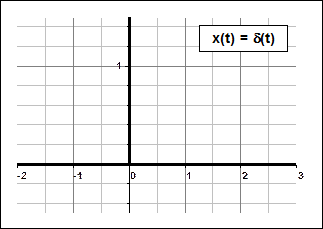
а) б)

Рис. 2.4. Единичная ступенчатая функция а) и единичная импульсная функция б).

Математически эти функции описываются следующим образом:

; .

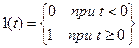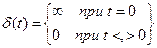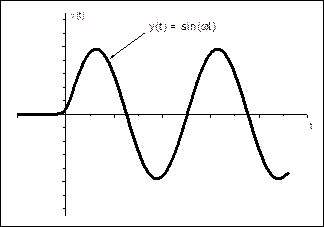
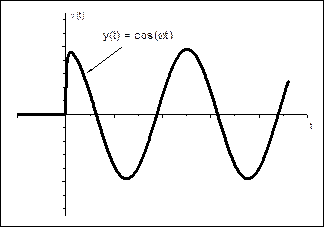
Рис. 2.5. Гармонические функции.

Динамической характеристикой любого элемента системы управления называется его реакция на типовое входное воздействие. В зависимости от вида типового воздействия разделяют временные и частотные характеристики.

Временные характеристики:

§ переходная характеристика h(t);

§ весовая функция или импульсная переходная функция w(t).

Частотные характеристики:

§ амплитудно-фазовая частотная характеристика (АФЧХ) или частотная передаточная функция;

§ амплитудная частотная характеристика (АЧХ);

§ фазовая частотная характеристика (ФЧХ);

§ логарифмическая амплитудная частотная характеристика (ЛАЧХ либо ЛАХ);

§ логарифмическая фазовая частотная характеристика (ЛФЧХ либо ЛФХ).

Перечисленные выше характеристики могут быть сняты экспериментально или построены по уравнению звена. Имеется и обратная возможность – по экспериментально полученным характеристикам составить уравнение звена. Кроме того, с помощью этих характеристик можно определить реакцию звена на любое возмущение произвольного вида. Эти характеристики являются исчерпывающим описанием динамических свойств звена.

123

Дата добавления: 2018-05-10; просмотров: 907;