Классическая электронная теория

Квантовая механика возникла не в результате свободного полета фантазии, ее создание было подготовлено всем предшествующим развитием физики. Вершиной этого развития явилась классическая электронная теория, созданная Г. Лоренцем (1853 – 1828). Эта теория основывалась на законах И. Ньютона (1643 – 1727) и Д. Максвелла (1831 – 1879). К 1900 г большинству ученых казалось, что физика в основном завершена, остались лишь отдельные пока не понятые факты и явления, которые должны найти объяснение в рамках существующей теории. Однако накапливались наблюдения, противоречащие великолепной электронной теории Лоренца. Попытки найти объяснение этим наблюдениям и привели к созданию квантовой механики, теории, которая качественно отлична от теории Лоренца, но дает совпадающие с ней результаты в тех случаях, когда эти результаты согласуются с опытом.

Зарождение качественно новых идей и представлений о мире в процессе анализа противоречий между предсказаниями существующей теорией и экспериментом является весьма поучительным. Для преподавателей физики важно не только знать основные идеи квантовой механики, но и понимать их происхождение. Назовем основные положения классической электронной теории, укажем ее достижения, а также трудности в объяснении отдельных явлений.

В электронной теории Лоренца рассматривается совокупность заряженных материальных точек, находящихся в вакууме. Порождаемое ими электромагнитное поле описывается уравнениями Максвелла. Движение частиц подчиняется законам Ньютона. Получается система уравнений, следствиями которой являются наблюдаемые движения заряженных частиц и порождаемые ими электромагнитные поля.

Из электронной теории, в частности, следует, что свет характеризуется объемной плотностью энергии u и объемной плотностью импульса 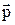, которые связанны соотношением u = с p. (1.1)

Свет может передавать свой импульс частицам тел, оказывая на них давление. Это предсказание теории Лоренца было подтверждено опытами П. Н. Лебедева (1866 – 1912).

Излучение света атомами трактуется в электронной теории как излучение переменного электрического диполя. В планетарной модели атома такой диполь образуют ядро и вращающийся вокруг него электрон. Частота колебания диполя, равная частоте вращения электрона, должна быть равна частоте излучаемого диполем света. Быстроту вращения электрона можно изменить, подействовав на него постоянным магнитным полем. Анализ влияния магнитного поля на вращение электрона в атоме позволил Лоренцу в 1897 г. объяснить нормальный (простой) эффект Зеемана. Этот эффект был открыт годом раньше С. Зееманом (1865 – 1943). Эффект заключается в расщеплении спектральных линий светящегося газа при помещении его в постоянное магнитное поле.

Следуя Лоренцу, покажем, что при наблюдении в направлении, перпендикулярном приложенному магнитному полю 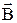, вместо излучения одной частоты w₀ должны наблюдаться излучения трех частот:

w = w₀ ±Dw, где Dw = 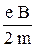. (1.2)

Частота w₀ определяется вторым законом Ньютона для электрона, вращающегося по круговой орбите радиуса r вокруг ядра атома:

m r w₀² = 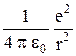, (1.3)

e и m – заряд и масса электрона.

Включение магнитного поля 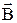, перпендикулярного плоскости орбиты, должно по закону электромагнитной индукции ускорить или замедлить движение электрона в зависимости от направления вращения. Новая частота w будет определяться условием:

m r w² = 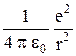± e w r B. (1.4)

Второе слагаемое представляет собой силу Лоренца, действующую на электрон со стороны магнитного поля. Из (1.3) и (1.4) следует (1.2), если учесть, что Dw<<w₀.

В светящемся газе атомы имеют всевозможную ориентацию. Поэтому в перпендикулярном к полю 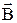направлении будут наблюдаться не только излучения частот (1.2), но и излучение частоты w₀. Это излучение обусловлено электронными орбитами, в плоскости которых лежит вектор 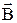. Включение магнитного поля не меняет магнитный поток через такие орбиты, он остается равным нулю. В результате в направлении, перпендикулярном полю 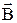, будут фиксироваться три частоты (триплет). Детальное рассмотрение [2] позволяет заключить, что при наблюдении вдоль магнитного поля 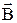должно регистрироваться излучение только двух частот (1.2) (дублет). Теория объясняет также характер поляризации излучений.

Заключения Лоренца относительно влияния магнитного поля на излучение атомов согласуются с наблюдениями Зеемана. Это рассматривалось как блестящее достижение классической теории. Однако последующие исследования выявили факты, которые не может объяснить теория Лоренца. В некоторых случаях наблюдалось расщепление не на Лоренцев триплет или дуплет, а на большее число линий. Такая картина получила название аномального (сложного) эффекта Зеемана. Аномальный эффект Зеемана не может быть объяснен классической теорией.

Помимо неспособности классической теории разобраться с аномальным эффектом Зеемана она обладает еще одним более существенным изъяном. Ее представление о движении электронов по окружностям противоречит закону сохранения энергии. Излучение, обусловленное движущимся по орбите электроном, уменьшает энергию атома, вследствие чего электрон должен упасть на ядро. Это должно произойти за время » 10^–7 с. Об этом существенном недостатке теории Лоренц писал в1924 г.: «Сегодня, излагая электромагнитную теорию, я утверждаю, что движущийся по орбите электрон излучает энергию, а завтра я в той же аудитории говорю, что электрон, вращаясь по орбите вокруг ядра, не теряет энергии. Где же истина? Способны ли мы вообще узнать ее, и имеет ли смысл заниматься наукой? Я потерял уверенность, что моя научная работа вела к объективной истине. Жалею только, что я не умер несколько лет тому назад, когда мне еще все представлялось ясным».

? Контрольные вопросы

1. Что такое квантовая механика в узком смысле слова?

2. Что такое квантовая механика в широком смысле слова?

3. Чем было обусловлено создание квантовой механики?

4. На каких положениях базируется электронная теория Лоренца?

5. Назовите явления, которые объясняются электронной теорией Лоренца.

6. Чем обусловлено расщепление спектральных линий светящегося газа при помещении его в магнитное поле?

7. В чем заключается аномальный эффект Зеемана?

8. Расскажите о проблеме устойчивости атомов с точки зрения классической теории.

F

Задания

Д.1. Давление света.

Плотность энергии и плотность импульса электромагнитных волн. Почему свет оказывает давление на тела? Как давление света зависит от плотности энергии излучения и коэффициента отражения поверхности? Опыты Лебедева.

1.1. Рубиновый лазер излучает в импульсе длительностью t = 0,1 мс энергию E = 10 Дж в виде узкого параллельного монохроматического пучка света. Найти среднее за время импульса давление такого пучка p_ср, если его сфокусировать в пятнышко диаметром d = 10 мк на поверхность, перпендикулярную пучку, с коэффициентом отражения r = 0,5.

p_ср = 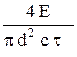(1 + r) = 65 атм.

1.2. Наблюдается одна из спектральных линий источника, находящегося в магнитном поле B = 1 Тл. Определить ее длину волны l, если интервал между компонентами этой линии Dl = 0.035 нм.

l = 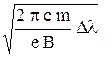= 0, 613 нм

1.3. Энергия I, излучаемая в единицу времени диполем 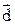, равна: I = 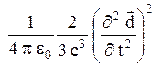. Полагая начальный радиус электронной орбиты равным r₀ = 0,5 10^–10 м, оцените время жизни t атома водорода.

t = 4 (p e m)² (c r₀)³/ e⁴ = 10^–11 с.

Равновесное излучение. Гипотеза Планка

& Литература: [2], [5].

Не смогла электронная теория Лоренца объяснить и закономерности теплового излучения. Попытки решить проблему теплового излучения привели к появлению в физике качественно новой идеи – идеи квантования и новой фундаментальной константы – постоянной Планка.

Исследуя свойства теплового излучения, Кирхгоф установил, что отношение энергии, излучаемой телом с единицы поверхности, к энергии, поглощаемой им, является для всех тел одной и той же (универсальной) функцией частоты n и температуры T (закон Кирхгофа). Следовательно, эта функция характеризует само излучение, а не излучающее тело. Чтобы установить вид этой функции, нужно исследовать излучение абсолютно черного тела, то есть такого, у которого поглощательная способность равна единице (все падающее на него излучение поглощается). Таким образом был экспериментально установлен вид спектральной светимости абсолютно черного тела R(n,T), то есть энергии, которая излучается единицей поверхности абсолютно черного тела по всем направлениям в единичном интервале частот.

Можно показать, что спектральная светимость абсолютно черного тела связана со спектральной объемной плотностью самого излучения r(n,T) простым соотношением: r(n,T) = 4 R(n,T) / c, (2.1)

где c – скорость света. Аналогичным образом связаны и интегральная объемная плотность излучения u и интегральная светимость R:

u (T) = 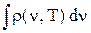, R(T) = 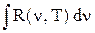, u(T) = 4 R(T) / c. (2.2)

Температурные зависимости величин u и R подчиняются закону Стефана–Больцмана:

u(T) = s1× T, R(T) = s ×T⁴ _, (2.3)

где s = 5, 67·10^–8 Вт / (м² К⁴) – постоянная Стефана–Больцмана, а постоянная s1 = 4 s / c.

Задача теории – получить согласующиеся с экспериментом функции r(n,T) и u (T). Релей и Джинс, используя положение классической физики о том, что на каждую волну равновесного излучения приходится в среднем энергия k T, получили формулу: r(n,T) = 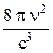k T, (2.4)

Формула Релея–Джинса (2.4) согласуется с экспериментом только при малых значениях n, а при больших частотах дает неограниченное возрастание r(n,T), что немыслимо для равновесного излучения («ультрафиолетовая катастрофа»).

М. Планк вначале эмпирическим путем подобрал подходящую формулу для r(n,T), а затем показал, что эта формула получается, если предположить, что электромагнитные волны, излучаемые атомами, могут принимать лишь значения энергии, кратные минимальной порции, пропорциональной частоте: e₀ = h n. Так получилась знаменитая формула Планка для спектральной плотности равновесного излучения:

r(n,T) = 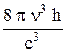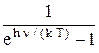. (2.5)

Для сравнения с экспериментом вместо функции r(n,T) удобнее использовать функцию r _l(l,T), которая связана с (2.5) соотношением: r _l(l,T) dl = r(n,T) dn.

Введенный Планком коэффициент пропорциональности h (постоянная Планка) может быть вычислен путем сопоставления формулы (2.5) с опытом. Так в физике появилась фундаментальная константа, характерная для квантовой физики.

? Контрольные вопросы

1. Что такое равновесное излучение?

2. Расскажите о законе Кирхгоффа и об абсолютно черном теле.

3. Что такое спектральная плотность равновесного излучения? Как она получается из опыта?

4. Нарисуйте графики зависимости спектральной плотности равновесного излучения r(n,T) и r _l(l,T) а также графики по формуле Рылея–Джинса.

5. Расскажите об ультрафиолетовой катастрофе.

6. Как Планку удалось получить формулу, правильно описывающую спектральную плотность равновесного излучения?

F

Задания

Д.2.1 Спектральная плотность равновесного излучения. Формула Планка. Равновесное излучение. Абсолютно черное тело. Зависимость спектральной плотности равновесного излучения от частоты и от длины волны. Закон смещения Вина. Закон Стефана-Больцмана. Формула Релея–Джинса. Формула Планка.

2.1. Получите из формулы Планка закон Стефана–Больцмана. Вычислите постоянную Стефана–Больцмана s, входящую в (2.3).

2.2. Получите из формулы Планка закон смещения Вина. Найдите постоянную Вина b = T lm, где lm – длина волны, соответствующей максимуму спектральной плотности r _l(l,T).

b = 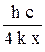= 2,9·10^–3 м К, где x – корень уравнения x = 5 (1 – e^–x ).