Приближенные методы расчета толщины защитных экранов от нейтронного излучения
При рассмотрении расчета защиты от нейтронного излучения следует иметь в виду процессы взаимодействия нейтронов с веществом среды.
Защита от нейтронного излучения основывается на поглощении тепловых нейтронов. Быстрые нейтроны должны быть сначала замедлены.
Нейтроны с энергией свыше 0,5 МэВ рассеиваются на ядрах поглощающей среды, испытывая неупругие столкновения с выходом нейтронов меньшей энергии. При этом ядра переходят в возбужденное состояние и возвращаются в основное состояние, испуская γ-излучение или β-частицы.
Нейтроны, имеющие энергию до 0,5 МэВ, испытывают в основном неупругое рассеяние.
В результате неупругого рассеяния нейтроны замедляются до тепловых и приходят в тепловое равновесие с окружающей средой. Тепловые нейтроны, диффундируя в защите, могут либо выйти за ее пределы, либо быть поглощенными в самой защите. При этом возникает захватное γ-излучение, которое необходимо учитывать при расчете защиты.
Под действием нейтронного облучения многие материалы активируются. Это следует учитывать при выборе защиты.
Ослабление узкого моноэнергетического пучка быстрых нейтронов происходит по экспоненте:
φх = φ exp(-Σtx), (6.26)
где φх — плотность потока нейтронов. нейтр./(м2·с), после ослабления в защите толщиной х, см; φ—плотность потока без защиты;
Σt—-полное макроскопическое сечение защитного материала, см-1;
Σt=σtnA (nА — число ядер, находящихся в 1 см3 поглощающего вещества, nА=ρ·6,023 1023/A), где А — атомная масса поглощающего вещества.
Для сложного состава защиты
Σt = σ1nA1 + σ2nA2+··, (6.27)
где σ1, σ2 — микроскопические сечения отдельных элементов, входящих в состав сложного вещества, см2; пA1, nA2 — числа ядер отдельных элементов, находящихся в 1 см3 вещества.
Ослабление плотности потока нейтронов в зависимости от толщины защиты х и длины релаксации нейтронов λ может быть определено по формуле
φχ = φ еxρ(-x/λ), (6.28)
где λ= 1/Σ.
Форма кривой ослабления (на начальном участке от источника в 2-3 длины релаксации) может отличаться от экспоненциальной формы. Это отличие учитывается введением коэффициента f. Для источников нейтронов спектра деления f ≈ 1.
Тогда плотность потока нейтронов от моноэнергетического точечного изотропного источника за защитой толщиной x (защита находится между источником и детектором) будет равна
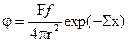 (6.29)
(6.29)
где F — поток нейтронов, нейтр./с.
При расчете защиты от быстрых нейтронов можно использовать величину слоя
половинного и десятикратного ослабления
Δ1/2 = 0,693/Σ и Δ1/10 = 2,303/Σ· (6.30)
Зная кратность ослабления (отношение какого-либо параметра, например плотности потока без защиты, к аналогичной величине с защитой)
k = φ/φx = exp(Σx) = 2n· 10n, (6.31)
можно найти толщину защитного слоя
х = пΔ1/2 + пΔ1/10 . (6.32)
Для расчета водной защиты от лабораторных (α,n)-источников нейтронов можно
использовать номограммы.
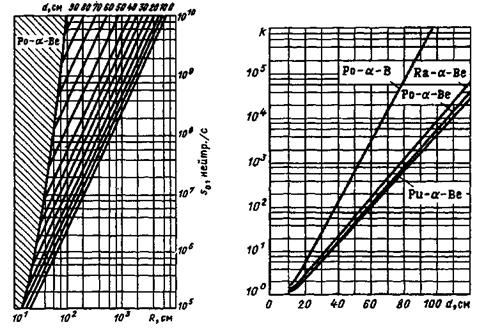
| Рис. 6.14. Номограмма первого типа для расчета защиты от нейтронов Ро-α-Ве-источника. | Рис. 6.15. Номограмма второго типа для расчета кратности ослабления нейтронов разных источников. |
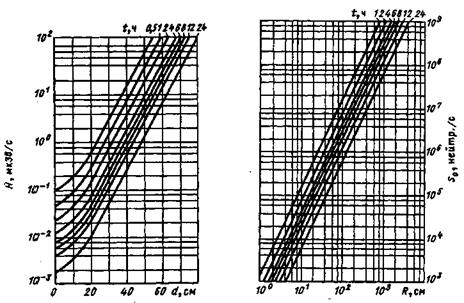
| Рис. 6.16. Номограмма третьего типа для расчета защиты от нейтронов Ρο-α-Ве-источника в зависимости от мощности дозы и t. | Рис. 6.17. Номограмма четвертого типа для расчета защиты без экранов. |
Первая номограмма (рис.6.14) построена для допустимой эквивалентной дозы профессионального облучения 0,0167 сЗв (0,0167 бэр) вдень, время облучения t=6 ч в день Она связывает между собой поток излучения S0, нейтр./с, расстояние от источника до точки детектирования R, см, и толщину водной защиты d, см. Номограмма построена для Ро-Ве-источника.
Вторая номограмма (рис.6.15) показывает зависимость кратности ослабления k от толщины водной защиты d, см, для Po-B-, Ra-Be-, Po-Be- и Ри-Ве-источников.
Третья номограмма (рис.6.16) построена для допустимой эквивалентной дозы профессионального облучения 0,0167 сЗв (0,0167 бэр) в день. Она связывает между собой измеренную или рассчитанную мощность эквивалентной дозы, мкЗв/с , расстояние от источника до детектора d, см, и время облучения t, ч, в сутки. Номограмма построена для Ро-Ве-источника.
Четвертая номограмма (рис.6.17) связывает между собой поток нейтронов S0, нейтр./с; расстояние от источника до детектора R, см, и время облучения t,ч, в сутки. При любом сочетании этих параметров выполняются допустимые условия работы при профессиональном облучении без зашиты.
Первая и третья номограммы для Ро-Ве-источника могут быть использованы для Pu-Ве-источников. Неточность расчетов для Pu-Be источников может быть оценена по второй номограмме, по которой можно определить длину релаксации нейтронов. Длина релаксации вводе для различных нейтронных источников следующая: Po-B λ=6,3 см; Ra-Be λ=9,8 см; Po-Be λ=10,3 см; Pu-Be λ=10,5 см.
При использовании в качестве защитного материала парафина его длина релаксации меньше длины релаксации в воде в 1,2 раза для Ро-В-источника и в 1,6 раза для Po-Be- источника.
Защита отα- и β-излучений
Защита от внешних потоков α-частиц не представляет особых сложностей, т.к. обладая очень высокой плотностью ионизации, α-частицы теряют свою энергию и поглощаются в сравнительно тонких слоях вещества.
Для определения толщины слоя достаточно знать пробег α-частицы в данном веществе.
Средний пробег α-частиц можно рассчитать в приближении непрерывного замедления по формуле
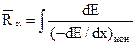 , (6.33)
, (6.33)
где (- dE/dx)ион — ионизационные потери энергии α-частиц. Защиту от внешних потоков α-частиц рассчитывают по максимальному пробегу Rα ≈ 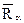 . Максимальный пробег α-частиц определяют также, используя приближенные эмпирические соотношения. Так, пробег в воздухе Rα,B, см для α-частиц, испускаемых естественными радионуклидами (E0= 4-7 МэВ), можно рассчитать по формуле
. Максимальный пробег α-частиц определяют также, используя приближенные эмпирические соотношения. Так, пробег в воздухе Rα,B, см для α-частиц, испускаемых естественными радионуклидами (E0= 4-7 МэВ), можно рассчитать по формуле
Rα,B =0,31Е03/2. (6.34)
где E0 — энергия α-частиц, МэВ.
Для среды x пробег α-частиц Rα,х, см, можно рассчитать по формуле
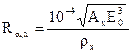 , (6.35)
, (6.35)
где E0— энергия α-частиц, МэВ; Ax, рх — атомная масса и плотность среды х, г/см3.
Для многокомпонентных по составу сред расчет массового пробега Rα, г/см2, можно выполнить по формуле
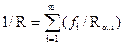 , (6.36)
, (6.36)
где Rα,i — пробег α-частицы в материале i-го компонента, г/см2, с весовым содержанием fi,
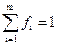
Проникающая способность α-частиц в средах невелика. Так, в воздухе пробег α-частиц, испускаемых, например, 222Rn (E0=5,5 МэВ), примерно равен 4см. Тем не менее при энергии Ео>7,5 МэВ пробег α-частицы в биологической ткани может превысить толщину слоя эпидермиса кожи (70 мкм) и достичь чувствительных клеток базального слоя.
Таким образом, для защиты от внешних потоков α-частиц достаточно тонких защитных экранов (тонкой фольги, листа бумаги, хирургических перчаток и т.п.).
Основная проблема здесь возникает при работе с открытыми α-излучателями. В этих задачах необходима защита внешней среды от загрязнения ее радиоактивными веществами и предотвращения их попадания внутрь организма.
Проблема защиты собственно от электронов, позитронов и β-частиц в диапазоне энергий радионуклидных источников также не существует в связи с их небольшими пробегами в среде. Главная задача здесь состоит в защите от вторичного тормозного излучения, выход которого зависит от энергии β-частиц и атомного номера среды. Важная характеристика электронов и β-частиц при прохождении их в веществе — пробег, определяющий их проникающую способность. Различают три пробега электронов в веществе: средний Rβ максимальный Rβmax и экстраполированный (или практический) Rэкс.
Максимальный пробег моноэнергетических электронов — минимальная толщина слоя вещества, при которой ни один из электронов, падающих нормально на слой, из него не вылетает. На практике, однако, из-за трудности однозначного определения Rβmax находят так называемый экстраполированный пробег, который получается в точке пересечения экстраполированного линейного участка кривой с осью абсцисс (штриховая линия на рис.6.18). Средний пробег (или просто пробег) можно определить из формулы (6.33).
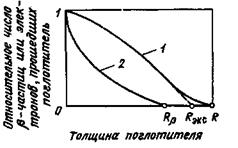
Рис. 6.18. Зависимость относительного числа моноэнергетических электронов (1) и β-частиц (2) прошедших поглотитель от толщины поглотителя.
На практике для расчета пробега β-частиц часто используют эмпирические зависимости. Так, максимальный пробег β-частиц в алюминии RA1, г/см2, с энергией в диапазоне 0,5 — 3 Мэв с погрешностью + 5% рассчитывается по формуле
RA1 = 0,52 Еβ — 0,09, (6.37)
где Eβ — граничная энергия β-частиц, МэВ.
По пробегу β-частиц в алюминии RA1, рассчитывают их массовый пробег Rx в любом веществе:
Rx = RA1(Z/A)A1/(Z/A)x, г/см2. (6.38)
Грубаяоценка максимальных пробегов β-частиц в алюминии и воздухе Rβmax, см, может быть получена из соотношений
RA1≈ 0,25Eβ; Rвозд≈ 400Eβ, (6.39)
где Eβ выражено в МэВ.
Пробег β-частиц в любой среде приблизительно во столько раз меньше или больше их
пробега в воздухе, во сколько раз плотность данной среды больше или меньше плотности
воздуха:
Rсреды/Rвозд=rвозд/rсреды <6·40)
Ослабление плотности потока β-частиц в поглотителе (кривая 2 на рис.6.18) приближенно подчиняется экспоненциальному закону
φ(d) = φоехр(-μmd), (6.41)
где d — массовая толщина поглотителя, г/см2; μm — массовый коэффициент поглощения электронов, см2/г.
Значения массового коэффициента поглощения μm, см2/г, могут быть определены приближенно из следующей зависимости от граничной энергии β-частиц Eβ , МэВ:
μm =15,5 Εβ-1,41 ≈17 Εβ-1,43 ≈ 22 Eβ-1,33. (6.42)
Защита от тормозного излучения электронов и β-частиц
При прохождении через вещество электроны и β-частицы расходуют свою энергию на ионизационные и радиационные потери. Механизм радиационных потерь состоит в торможении β-частиц (электронов) внешним полем ядер или электронов поглотителя, приводящим к образованию тормозного излучения. Для расчета защиты от тормозного излучения необходимо знать его выход и энергетическое распределение. Строгой теории, позволяющей рассчитать эти величины, нет. На практике для оценки можно пользоваться следующими приближенными формулами: при торможении β-частиц для выхода тормозного излучения Yβ, МэВ/расп.,
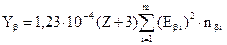 , (6.43)
, (6.43)
Для моноэнергетических электронов Yc, МэВ/расп., вычисляется из соотношения
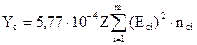 , (6.44)
, (6.44)
где Z — атомный номер вещества, в котором происходит торможение электронов; Eβi и Eci — граничная энергия β-излучения и энергия моноэнергетических электронов i-й энергетической группы соответственно, МэВ; nβiи пci — выход β-частиц и моноэнергетических электронов на один распад ядра соответственно; т — число энергетических групп β-частиц или моноэнергетических электронов в спектре излучения радионуклида.
Формулы (6.43), (6.44) получены в предположении полного поглощения β-частиц и электронов в веществе зашиты.
Для сложных химических соединений, в состав которых входит l разных элементов, используют среднее значение Z:

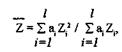 (6.45)
(6.45)
где аi — доля общего числа атомов соединения, имеющих атомный номер ΖΓ
Соотношение (6.43) записано для радионуклидов, форма β-спектра которых сходна с β-спектром 32P. Для радионуклидов с отличающейся формой β-спектра погрешность расчетов по этой формуле растет, достигая, например, для 35S 42%. В меньшей степени форма β-спектра отражается на результатах, полученных по формуле

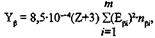 (6.46)
(6.46)
где Εβί — средняя энергия β-частиц i-й энергетической группы, МэВ.
Энергетическое распределение тормозного излучения для β-частици моноэнергетических электронов приведено в табл. 6.3.
Таблица 6.3.
Дата добавления: 2018-05-10; просмотров: 1808;











