Цикл Карно и его к.п.д. для идеального газа

Круговые процессы (циклы)

Первое начало термодинамики, являющееся законом сохранения энергии, не указывает направления возможного протекания процессов. Любой процесс, при котором не нарушается закон сохранения энергии, возможен с точки зрения I начала термодинамики. Второе начало термодинамики позволяет уточнить направление протекания процессов. Его применение требует четкого разграничения обратимых и необратимых процессов.

Обратимым процессом называется такой процесс, который может протекать как в прямом, так и в обратном направлениях. Если при прямом ходе на каком-то элементарном участке система получаем тепло dQ и совершает работу dA, то при обратном ходе на этом участке отдает тепло dQ’ = dQ и над ней совершает работу dA’ = dA. При обратимом процессе в окружающих систему телах не должно оставаться никаких изменений, обратимые процессы являются физической абстракцией. Все реальные процессы необратимы. Некоторые характерные примеры необратимых процессов: расширение газа в пустоту, диффузия, теплообмен и т.д. Для возвращения системы в начальное состояние во всех этих случаях необходимо совершить работу с использованием внешних сил.

Важное значение в термодинамике имеют так называемые круговые (или замкнутые) процессы, в результате которых система после ряда изменений возвращается в первоначальное положение. Круговые процессы иначе называются циклами.

График цикла представляет собой замкнутую линию. На рис.11.1 изображен прямой цикл. Он соответствует тепловой машине, т.е. устройству, которое получает количество теплоты от некоторого тела – теплоотдатчика (нагревателя), совершает работу и отдает часть этой теплоты другому телу – теплоприемнику (холодильнику).

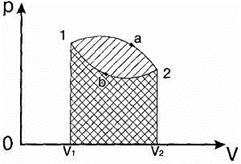
Рис.11.1

В этом цикле при сообщении теплоты газу, он расширяется (dV > 0) и совершает положительную[1] работу А₁, которая численно равна площади под кривой 1а2. В процессе 2б1 газ сжимается (dV < 0) и совершает отрицательную работу А₂, численно равную площади под кривой2б1.

Алгебраическое суммирование работ (А = А₁ + А₂) дает в целом положительную работу, совершаемую газом за цикл. Эта работа численно равна площади замкнутой кривой 1а2б1.

Применим к круговым процессам первое начало термодинамики. Для процесса 1а2 оно будет иметь вид

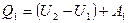(11.1)

где Q₁ – теплота, передаваемая газу от нагревателя; U₁ и U₂ – внутренняя энергия газа в точках 1 и 2; А₁ – работа, совершаемая газом.

При сжатии газ совершает работу А₂ и отдает тепло Q₂, что равнозначно получению -Q₂. Для процесса 2б1 уравнение первого начала термодинамики имеет вид

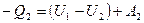(11.2)

При сложении уравнений (11.1) и (11.2), получим

Q₁ – Q₂ = A₁ + A₂ или Q₁ – Q₂ = A (11.3)

где А = A₁ + A₂.

При сообщении системе теплоты Q₁ только часть ее превращается в работу А, а часть Q₂ передается холодильнику. Поэтому термический коэффициент полезного действия h для кругового процесса равен

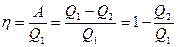(11.4)

Цикл называется обратным, если за цикл совершается отрицательная работа. Такой процесс протекает в направлении как показано на рис. 11.2.

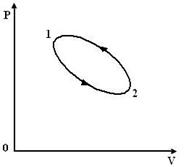
Рис.11.2

Обратный цикл соответствует работе холодильной машины, т.е. такой системе, которая отбирает теплоту от холодильника и передает нагревателю за счет работы внешних сил.

Цикл Карно и его к.п.д. для идеального газа

Французский инженер Сади Карно[2], работая над повышением к.п.д. тепловых машин, пришел к выводу, что газ совершает наиболее экономичный цикл, когда он состоит из двух изотерм и двух адиабат.

Цикл Карно для идеального газа представлен на рис. 11.3.

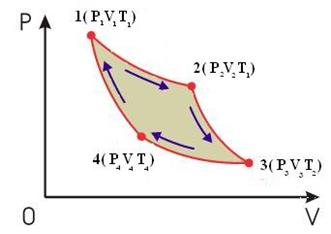
Рис.11.3

Из состояния 1 газ, получив от нагревателя Q₁, расширяется изотермически (Т₁ = const) и переходит в состояние 2. Из состояния 2 газ переводится в состояние 3 адиабатически. Здесь работа расширения происходит за счет убыли внутренней энергии, поэтому температура падает до Т₂. Переходя из состояния 3 в состояние 4 газ изотермически сжимается, отдавая холодильнику количество теплоты Q₂. При переходе из состояния 4 газ адиабатически сжимается до первоначального состояния 1.

Подсчитаем к.п.д. для описанного цикла Карно.

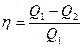(11.4)

При изотермическом расширении газа на участке 1-2 работа совершается за счет Q₁

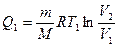(11.5)

На участке 3-4

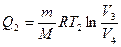(11.6)

Подставив (11.5) и (11.6) в (11.4), получим

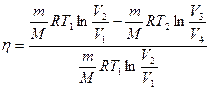(11.7)

Можно доказать, что

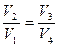(11.8)

Запишем уравнения адиабаты для адиабатических процессов на участках 2-3 и 4-1

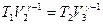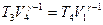и (11.9)

Из уравнений (10.9) нетрудно получить уравнение (11.8). Следовательно, в уравнении (11.7) 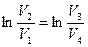. После соответствующих сокращений, к.п.д. цикла Карно выразим, используя значения температуры нагревателя Т₁ и холодильника Т₂.

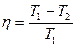(11.10)

Отсюда видно, что термический к.п.д. цикла Карно не зависит от природы газа (рабочего тела) и является только функцией температур нагревателя и холодильника. Это утверждение носит название теоремы Карно.

Термический к.п.д. цикла Карно равен к.п.д. кругового процесса для обратимого и больше для необратимого цикла, т.е.

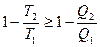(11.11)