Приведенное количество теплоты. Энтропия

Как уже говорилось выше, термический к.п.д. для обратимого цикла

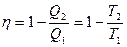(11.12)

Отсюда

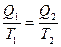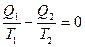или (11.13)

Учитывая, что теплота Q₂ отрицательна, выражение (11.13) примет вид

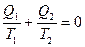(11.14)

где 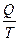называется приведенным количеством теплоты. Из выражения (11.14) следует, что для цикла Карно алгебраическая сумма приведенных количеств теплоты равная нулю. Для любого обратимого цикла

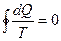(11.15)

где 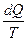– приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса.

Если интеграл по замкнутому контуру равен нулю, то подынтегральное выражение является некоторой функцией состояния, не зависящей от пути.

Функция состояния, дифференциалом которого является 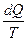, называется энтропией S, т.е.

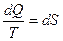(11.16)

Для обратимого процесса DS = 0, для необратимого DS > 0, т.е. в общем случае

DS ≥ 0 (11.17)

Выражение (11.17) называется неравенством Клаузиуса и означает, что энтропия замкнутой системы либо возрастает, либо остается неизменной (энтропия не убывает). Реальные процессы необратимы, а следовательно, энтропия только возрастает. Это еще одна формулировка II начала термодинамики.

Опираясь на эту формулировку и на свой вывод о том, что все формы движения должны перейти в тепловую, Клаузиус пришел к выводу о неизбежности так называемой тепловой смерти Вселенной. Суть которой состоит в наступлении полного теплового равновесия в результате перехода тепла от более нагретого тела к менее нагретому.

Ошибочность такого вывода состоит в том, что II начало термодинамики применимо только к замкнутым системам. Такая безграничная и бесконечно развивающаяся система как вселенная не является замкнутой.

Физический смысл энтропия объяснил Больцман. Он же установил связь энтропии S с термодинамической вероятностью состояния системы

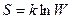(11.17)

где k – постоянная Больцмана; W – термодинамическая вероятность, т.е. количество микросостояний, который определяют данное состояние.

Формула Больцмана (11.17) определяет статистический смысл энтропии, как меры неупорядоченности системы. В замкнутой системе процессы протекают в направлении увеличения количества возможных микросостояний. Иначе формулируя – система стремится от менее вероятного, к более вероятному неупорядоченному состоянию. Исходя из этого, можно дать еще одну формулировку II начала термодинамики: в замкнутой системе при обратимых провесах растет вероятность состояний, а при обратимых процессах, она остается неизменной.

[1] Напомним, что работа системы (в данном случае, газа) считается положительной, когда сама система совершает работу и отрицательной, когда работа совершается над системой внешними силами.

[2] Карно Накола Леонард Сади (1796-1832), французский физик и инженер.