Вдавливание в горную породу жесткой сферы

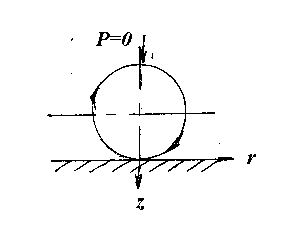Рис.30

Если нагрузка, приложенная к сфере, равна нулю (т.е. Р = 0), то контакт этой сферы с поверхностью породы будет осуществляться в точке (рис.30).

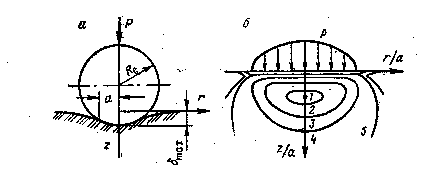
Рис.31

В случае приложения нагрузки на сферу контакт между сферой и горной породой будет происходить по круглой площадке, радиус которой можно подсчитать по формуле:

.

В центре площадки давления, т. е. по оси Z будет максимальное давление, которое подсчитывается так:

.

При удалении от центра к периферии величина давления (Р) изменяется (уменьшается) по следующему закону:

.

Перемещение вглубь тела (первоначальной) точки контакта зависит от величины приложенной нагрузки и определяется по формуле:

.

При вдавливании сферы область всестороннего сжатия значительно меньше, чем при вдавливании цилиндрического пуансона. Область максимальных касательных напряжений в этом случае находится на оси симметрии (ось Z) и на некоторой глубине, равной » 0,5а, а также на контуре давления.

Графически эта картина выглядит так, как представлено на рис.31 б.

Максимальные касательные напряжения по оси симметрии можно подсчитать по формуле:

,

где .

Если мы будем вдавливать прямоугольный штамп, то картина максимальных касательных напряжений будет выглядеть так, как это показано на рис.32. (Также в относительных единицах).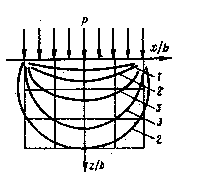

Рис.32