Модель идеального смешения (МИС)

Предполагается, что любая порция входящего в аппарат меченых элементов потока мгновенно и равномерно перемешивается во всем объеме. Таким образом, концентрация меченых элементов потока одинакова во всех точках аппарата. По аналогии с (2.31) (источника нет) можно записать:

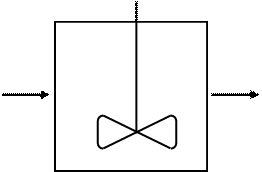Рис. 2.13 Модель идеального смешения (схема потока)

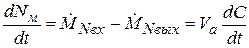, (2.149)

где 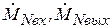– количество меченых элементов потока, входящих в аппарат и выходящих из него за единицу времени.

При любых значениях t>0 , входа меченых элементов в аппарат не будет, т.е. 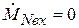. Тогда

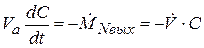. (2.150)

Имея, в виду 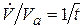получим:

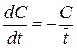и разделяя переменные:

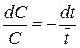. (2.151)

Интегрируя уравнение (2.151) с начальными условиями С(Q)=С₀ получим:

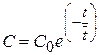. (2.152)

Переходя, к безразмерной функции распределения имеем:

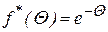. (2.153)

На рис. 2.14 изображена зависимость f^*(Q) от Q по формуле (2.153).

Рис. 2.14 Вид функции распределения f^*(Q) для МИС

К аппаратам идеального смешения близки аппараты с интенсивным перемешиванием и аппараты с псевдоожиженным слоем.

Структуры потоков в промышленных аппаратах не соответствует ни МИВ, ни МИС. Реальные аппараты промежуточного типа.