Общая характеристика блочных кодов

Рассматриваемые коды называются линейными потому, что кодирование и декодирование в них сводятся к применению некоторых линейных алгебраических операций.

Разрядность блока, т.е. длина кодовой комбинации, подбирается так, чтобы множество блоков этой длины существенно превышало множество кодируемых комбинаций. При этом имеется возможность однозначно сопоставлять кодируемые комбинации с некоторыми подобранными по определенным правилам комбинациями помехоустойчивого кода. Последние называются разрешенными, и именно они передаются по каналу связи. Остальные комбинации называются неразрешенными и на выходе канала связи могут появляться только в результате искажения передаваемых разрешениях.

Таким образом, прием неразрешенной комбинации свидетельствует о наличии в ней ошибки. Указанные свойства кода используются для обнаружения ошибок в принимаемых комбинациях. Кроме того, многие коды дают возможность исправлять некоторые ошибки за счет избыточности, заключенной в принимаемой комбинации.

Количество искаженных символов в кодовой комбинации (блоке) - это кратность ошибки. Код называется совершенным, если вся его избыточность расходуется на исправление ошибок кратности S и код не исправляет ни одной ошибки более высокой кратности. В теории кодирования оптимальным (плотноупакованным) называется код, который обеспечивает наименьшую вероятность ошибочного декодирования среди кодов той же длины и избыточности.

Во многих случаях вероятность кратной ошибки тем меньше, чем больше кратность последней. Поэтому многие коды рассчитаны на исправление ошибок небольшой кратности в первую очередь, одиночных. В случаях, когда наиболее вероятными являются пакеты ошибок, т.е. ошибок в разрядах, следующих друг за другом, применяются специальные коды, обладающие соответствующими свойствами.

В самом общем виде принцип коррекции ошибок сводится к следующему. Все множество комбинаций заданной разрядности разбивается на непересекающиеся подмножества, в каждом из которых заключена только одна разрешенная комбинация. При приеме неразрешенной комбинации она заменяется той разрешенной, которая находится в одном подмножестве с принятой неразрешенной. Способ разбиения всех возможных комбинаций на подмножества и определяет корректирующие свойства кода.

Для коррекции наиболее вероятных ошибок, т.е. ошибок малой кратности, следует принимать решение, что была передана та разрешенная комбинация, которая отличается от принятой наименьшим числом символов. Различие между комбинациями принято характеризовать расстоянием Хэмминга d, равным числу разрядов, в которых две комбинации имеют различные, т.е. не совпадающие символы. Например, комбинация 0100 отличается от комбинации 1000 в двух разрядах, следовательно, дистанция (расстояние) Хэмминга между этими комбинациями равна двум. Чем больше минимальное расстояние между разрешенными комбинациями кода (кодовое расстояние d₀), тем больше корректирующие возможности кода. Так, при кодовом расстоянии d₀ = 2 код дает возможность обнаруживать только одиночные ошибки, при d₀ = 3 - исправляет все одиночные ошибки или обнаруживает все одиночные и двойные ошибки. В общем случае для исправления ошибок кратности до S включительно кодовое расстояние должно удовлетворять условию d₀≥2S+1.

Пример. Множество трехразрядных комбинаций в трехмерном пространстве представляет собой множество вершин куба с длиной ребер, равной единице
(рис. 3.1).

Из рис. 3.1 ясно, что при необходимости исправления всех одиночных ошибок в качестве разрешенных следует выбирать две комбинации, соответствующие противоположным вершинам куба (например, 101 и 010 или 000 и 111). Если необходимо только обнаруживать одиночные ошибки, в качестве разрешенных можно брать комбинации, различающиеся в двух разрядах (например, 001, 010 и 111).

Рассмотрим кратко свойства наиболее широко применяемых кодов.

Групповые коды

Линейные групповые коды составляют самый большой класс блочных кодов. Основой математического описания линейных блочных кодов является линейная алгебра. Кодовые комбинации рассматриваются как элементы некоторого множества, в котором определены некоторые алгебраические операции.

В линейной алгебре группой называется множество элементов, в котором определена основная операция (обычно обозначается Å), причем она должна быть ассоциативной (aÅ(bÅc)=(aÅb)Åc), а для коммутативных групп (групп Абеля) - и коммутативной (aÅb = bÅa) и должна обладать обратной операцией. Группы, состоящие из конечного числа элементов, называются конечными. В конечной группе в результате операции, применяемой к любым элементам группы, должны образовываться также элементы этой группы. Последнее свойство называется свойством замкнутости.

Любой двоичный линейный код является групповым, так как совокупность входящих в него кодовых комбинаций образуют группу. В бинарных кодах в качестве основной и обратной операции принимается суммирование по модулю 2 (обозначается Å), а в качества нулевого элемента - комбинация, состоящая только из нулей.

Сложение и умножение элементов кода по модулю 2 (четности) производится по следующим правилам:

0 Å 0 = 0; 0 Å 1 = 1; 1 Å 1 = 0 (3.1)

0 ´ 0 = 0; 0 ´ 1 = 1; 1 ´ 1 = 1

Групповые коды бывают разделимыми (систематическими) и неразделимыми (несистематическими). В систематических кодах символы кодируемой комбинации (информационные символы) без изменения проставляются в заранее известные разряды избыточной комбинации, а в остальных разрядах располагают проверочные символы, которые определяют в результате проведения линейных алгебраических операций над информационными символами. В несистематических кодах все символы избыточной комбинации определяются в результате проведения алгебраических операций и не делятся на информационные и проверочные. На практике применяются преимущественно систематические коды.

Ознакомимся подробнее с теорией двоичных систематических кодов. Проверочные символы в этом случае находятся путем следующих алгебраических операций. Суммируется по модулю 2 количество единиц в определенных информационных разрядах и добавляется такое значение проверочного символа (1 или 0), чтобы вся сумма по модулю 2 была равна нулю, т.е., чтобы общее количество единиц было четным. Такое равенство называют проверочным. При декодировании проверяется выполнение этих равенств. Невыполнение хотя бы одного из них означает ошибку в принятой комбинации.

Количество информационных символов N₀ = 2ⁿ – 1 или число разрядов двоичного кода n, общая длина (число разрядов) всей закодированной комбинации m = n + r, где r – число разрядов проверочных (избыточных), что составляет в двоичном коде 2^m = N разрешенных кодовых комбинаций. Код обозначается (m, n).

Рассмотрим некоторые оценки в выборе параметров кода для обнаружения и исправления ошибки в системе передачи кодовых комбинаций.

Если имеется Е векторов ошибок, то число двоичных неразрешенных комбинаций, отличных от кодовых N₀ комбинаций будет очевидно E × N₀. С другой стороны, это число не должно превосходить числа N – N₀ всех возможных неразрешенных комбинаций. Следовательно, EN₀ ≤ N – N₀ и тогда

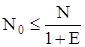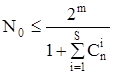; , (3.2)

где S – кратность ошибки (число неверно принятых разрядов),

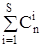- число сочетаний 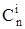возможных ошибок.

Для исправления однократной ошибки S = 1, 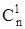= n и нижняя оценка

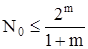, т.к. N₀ = 2ⁿ, то 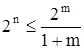(3.3)

Это условие выбора длины кода m при заданной длине информационного сигнала n. Зная n, вычислив m, можно определить разрядность проверочных символов r = m – n. Для n = 4 (N₀ = 2⁴ = 16),
m = 7, r = 3 код (7,4); для n = 5 (N₀ = 2⁵ = 32), m = 9, r = 4 код (9,5).

Для исправления двукратных ошибок S = 2, .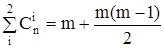

Для n = 4 (N₀ = 2⁴ = 16), m = 10, r = 6 код (10,4); для n = 5 (N₀ = 2⁵ = 32), m = 11, r = 5 код (11,5).