Построение групповых кодов, исправляющих одиночные ошибки
Вырабатываемое источником информации единичное сообщение формируется в безызбыточную комбинацию, причем все комбинации должны иметь одинаковую длительность (разрядность n).
Рассмотрим пример кодирования и исправления однократных ошибок групповым кодом Хемминга для n = 4 разрядных информационных блоков. Из условия (3.3.) следует, что m = 7, код (7,4) имеет семь разрядов, из них 4 информационных.
Построим "матрицу ошибок", т.е. переберем все возможные однократные ошибки (место ошибки определим вектором с одной единицей):
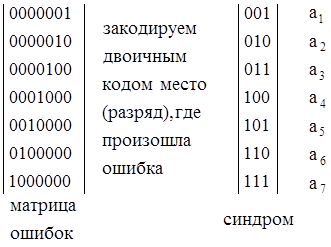 . (3.4)
. (3.4)
Указатель разряда, где есть ошибка, называют синдромом ошибки. При рассмотрении синдрома ошибки следует выделить первую, вторую и третью строки, которые указывают на возможные ошибки в первом, втором и четвертом разрядах. Синдромы этих разрядов в своем начертании имеют по одной единице, что позволяет выбрать эти разряды для размещения контрольных символов. Проверочные (кодовые) уравнения для них запишем по столбцам:
| а) | а1 Å а3 Å а5 Å а7 = 0 | б) | а1 = а3 Å а5 Å а7 | |
| а2 Å а3 Å а6 Å а7 = 0 | а2 = а3 Å а6 Å а7 | (3.5) | ||
| а4 Å а5 Å а6 Å а7 = 0 | а4 = а5 Å а6 Å а7 |
В качестве примера закодируем информационный блок 1010.
В выбранном 7 элементном блоке 1, 2, 4 разряды заняты под проверочные, а в 3, 5, 6, 7 разрядах запишем передаваемую информацию.
| а7 | а6 | а5 | а4 | а3 | а2 | а1 |
Найдем проверочные символы из уравнения (3.5,б)
а1 = а3 Å а5 Å а7 = 0 Å 1 Å1 = 0 а1 = 0
а2 = а3 Å а6 Å а7 = 0 Å 0 Å 1 = 1 а2 = 1
а4 = а5 Å а6 Å а7 = 1 Å 0 Å 1 = 0 а4 = 0
Теперь запишем закодированный блок
| а7 | а6 | а5 | а4 | а3 | а2 | а1 |
число 1010010.
Допустим, что при приеме этого блока произошла ошибка в третьем разряде (т.е. мы приняли блок вида 1010110), тогда проверочные равенства (3.5,а) в приемнике дадут синдром ошибки:
а1 Å а3 Å а5 Å а7 = 0 Å 1 Å 1 Å 1 = 1
а2 Å а3 Å а6 Å а7 = 1 Å 1 Å 0 Å 1 = 1
а4 Å а5 Å а6 Å а7 = 0 Å 1 Å 0 Å 1 = 0.
Полученный синдром 011 указывает, что ошибка произошла в третьем разряде, и, значит, третий разряд надо исправить (просто инвертировать на обратный знак). Так можно обнаружить и исправить любую однократную ошибку (в любом разряде).
Дата добавления: 2018-05-10; просмотров: 1276;











