Неустойчивые резонаторы (геометрическое приближение)

Резонаторы, для которых выполняются условия (7.5), называют неустойчивыми.

Физический смысл этого термина можно понять, если учесть, что к их числу относятся и резонаторы, образованные выпуклыми зеркалами (рисунок 7.6). Видно, что долго распространяться в резонаторе могут только фотоны, двигающиеся по оси резонатора. Малейшее отклонение от этого направления (а оно неминуемо уже в силу дифракции световой волны) приведет к вытеснению их из резонатора из-за его геометрии.

Первоначально часть разработчиков резонаторов (как теоретиков, так и экспериментаторов), необоснованно распространяя проведенное в предыдущем разделе рассмотрение на область, где не выполняются приближения, в которых это рассмотрение выполнено, сделали необоснованный вывод о бесперспективности использования таких резонаторов в лазерах. Однако исследования, проведенные Ю.А. Ананьевым и В.Н. Рождествиным в СССР и А.Е. Сигманом в США, показали, что неустойчивые резонаторы обладают рядом достоинств. В настоящее время эти резонаторы с успехом используются в мощных лазерах.

Как уже говорилось ранее, в неустойчивых резонаторах наблюдается «разбегание» излучения от оси резонатора, что ведет к появлению «геометрических» потерь, связанных с неминуемым в этом случае выходом излучения мимо краев зеркала резонатора (рисунок 7.7).

Для работы лазера в автоколебательном режиме необходимо выводить часть потока излучения в качестве выходного. В неустойчивых резонаторах в этом качестве можно использовать проходящее мимо краев зеркал излучение (такой вывод излучения называют дифракционным), так же, как в устойчивом резонаторе используется излучение, проходящее через частично пропускающее зеркало. При этом, подбирая геометрию резонатора, можно обеспечить оптимальный с точки зрения энергетических характеристик коэффициент вывода излучения.

Достоинством таких резонаторов является возможность хорошего заполнения активной среды излучением низших типов колебаний компактных активных объемов (характеризуемых большими значениями числа Френеля). Напомним, что в устойчивых резонаторах низшие поперечные моды сконцентрированы вблизи оси резонатора и используют активную среду малоэффективно.

Неустойчивые резонаторы из вышеприведенных соображений наиболее интересны для мощных лазеров. В медицине подобные лазеры на углекислом газе используются в аппаратах для лазерной реваскуляризации миокарда, когда требуются мощные импульсы излучения.

Неустойчивые резонаторы могут быть исследованы в рамках геометрического приближения. Рассмотрим резонатор, образованный двумя выпуклыми сферическими зеркалами (рисунок 7.8) З₁ и З₂, диаметрами 2а,расположенными на расстоянии L.

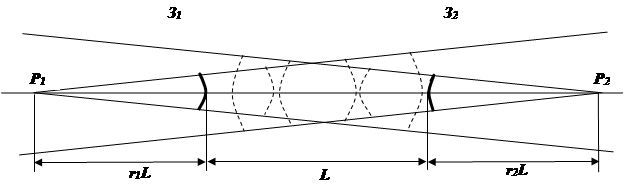
Рисунок 7.8. Распространение сферических волн в неустойчивом резонаторе

Пусть сферическая волна распространяется направо от зеркала З₁таким образом, как если бы она исходила из центра в точкеP₁ за зеркалом. В общем случае P₁ не совпадает с центром кривизны зеркала. Эта волна отражается от зеркала З₂и создает вторую сферическую волну с мнимым центром P₂, распространяющуюся налево. Положение центра P₂связано с положением центра P₁и кривизной зеркала З₂ формулами геометрической оптики. Новая сферическая волна, отразившись от зеркала З₁, образует в свою очередь сферическую волну с новым мнимым центром за этим зеркалом. Для собственного типа колебаний необходимо выполнение лишь одного требования: новый мнимый центр после полного прохода резонатора должен совпасть с первоначальным центром P₁ . Расчет дает пару центров, положение которых определяется формулой:

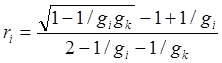, где i,k=1,2; i≠k. (7.7)

В этом случае однородная сферическая волна воспроизводит через один полный проход волну, подобную себе по форме, но несколько ослабленную вследствие того, что часть энергии выходит за края зеркал.

Пусть зеркала резонатора имеют одинаковую кривизну и одинаковые диаметры 2а.Если в этом случае распределение амплитуды излучения на поверхности первого зеркала описывается осесимметричной функцией f₁=f₁(х), где х – расстояние от оси резонатора. Поскольку в резонаторе распространяется расходящаяся сферическая волна, то после прохождения резонатора распределение излучения в плоскости второго зеркала будет иметь вид

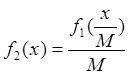, (7.8)

где M – величина линейного увеличения размера волнового фронта за проход, связанная с g–параметрами выражением

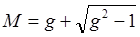. (7.9)

Появление М в знаменателе связано с тем, что плотность интенсивности сферической расходящейся волны ослабляется по мере увеличения фронта. Уравнение для собственных значений и собственных функций неустойчивого резонатора будет иметь вид

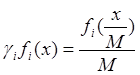(7.10)

Этому уравнению удовлетворяют решения вида

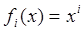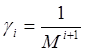, , (7.11)

где i – любое действительное число. Часто используемое ограничение значений i числами натурального ряда в данном случае не имеет места. Таким образом, при геометрическом рассмотрении мы получаем континуум собственных функций. Иначе говоря, геометрическое рассмотрение дает нам связь между распределением поля излучения в пространстве и его ослаблением в резонаторе.

Так, для равномерного распределения поля излучения потери за один проход составляют величину

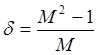. (7.12)

Интересно, что рассмотрению не противоречат не только дробные, но и отрицательные значения i. Более того, они имеют простой физический смысл. Представим себе не расходящуюся, а сходящуюся сферическую волну с теми же мнимыми центрами. В этом случае она тоже будет преобразовываться в резонаторе сама в себя. Плотность мощности подобной волны, если она каким-либо способом образуется в реальном лазерном резонаторе, будет возрастать, что может привести к повреждению его зеркал. Подобное может произойти, например, в неустойчивых конфокальных резонаторах (рисунок 7.9), часто называемых телескопическими.

В качестве выходного используется излучение, выходящее мимо краев выпуклого зеркала. Эти резонаторы интересны тем, что один из мнимых центров (на рисунке правый) расположен в бесконечности, то есть излучение, распространяется в этом направлении параллельным (с точностью до дифракционных ограничений) пучком, то есть имеет желательную для большинства применений минимальную расходимость. Для подобных резонаторов стал привычным термин «телескопические резонаторы». Именно в таких резонаторах наличие отражающих плоскостей, перпендикулярных оси резонатора, например, торцов активного элемента, может привести к появлению паразитной сходящейся волны.

Образование подобной волны в реальном резонаторе нежелательно, поскольку, не выходя наружу, она не только снимает часть инверсной населенности, но, стягиваясь к оси резонатора, она может создать высокую плотность мощности, способную повредить зеркала резонатора.

Для более детального рассмотрения свойств неустойчивых резонаторов необходимо воспользоваться уравнениями для комплексных амплитуд. Этому посвящен описанный ниже метод Прони.