Элементы электрических цепей синусоидального тока

Основные элементы электрических цепей синусоидального тока:

- источники электрической энергии (источники ЭДС и источники тока); резистивные элементы (резисторы, реостаты, нагревательные элементы и т.д.);

- емкостные элементы (конденсаторы);

- индуктивные элементы (катушки индуктивности).

3.2.1 Резистивный элемент (РЭ). На рисунке 3.4,а изображен РЭ, по которому течет ток

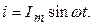(3.18)

По закону Ома напряжение РЭ

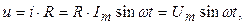(3.19)

где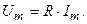

Из формул (3.18) и (3.19) следует вывод: ток и напряжение в рези-стивном элементе совпадают по фазе (изменяются синфазно). Это положение наглядно иллюстрируется на рисунке 3.4,б,в. Из формул (3.19) следует другой вывод: закон Ома выполняется как для амплитудных значений тока и напряжения:

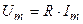, (3.20)

так и для действующих значений тока и напряжения:

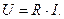(3.21)

Выразим мгновенную мощность р через мгновенные значения тока iи напряжения u:

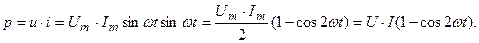(3.22)

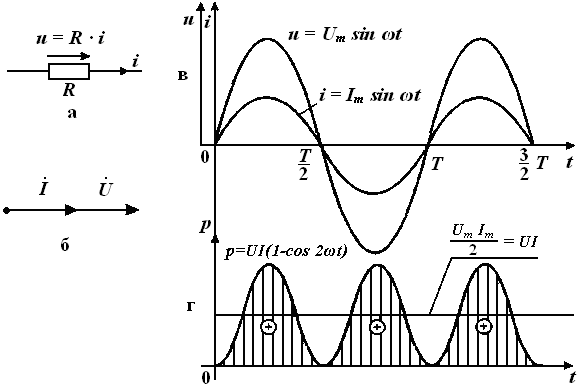
Рис. 3.4. Резистивный элемент: а) изображение на схеме; б) векторы тока и напряжения; в) графики тока и напряжения; г) график мгновенной мощности

График изменения мощности р со временем представлен на рис. 3.4,г. Анализ графика и формулы (3.22) позволяют сделать следующие выводы:

- мгновенная мощность р имеет постоянную составляющую

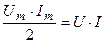и переменную составляющую 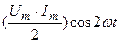, изменяющуюся с частотой ;

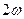- мощность в любой момент времени положительна 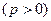,т.е. в резистивном элементе происходит необратимое преобразование электрической энергии в другие виды энергии («потребление» энергии);

- постоянная составляющая в формуле (3.22) есть среднее значение мгновенной мощности за промежуток времени равный периоду Т. Следовательно, энергия W, преобразуемая в резистивном элементе в течение периода, подсчитывается по формуле

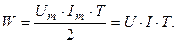(3.23)

Энергия, преобразуемая в резистивном элементе за любой промежуток времени от 0 до t определяется по формуле

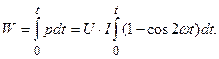(3.24)

3.2.2 Индуктивный элемент. Классическим примером индуктивного элемента (ИЭ) является катушка индуктивности – провод, намотанный на изоляционный каркас (рис. 3.5,а)

На рисунке 3.5,б изображен индуктивный элемент, по которому течет ток

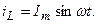(3.25)

Согласно закону электромагнитной индукции, напряжение на индуктивном элементе

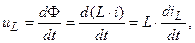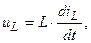т.е. (3.26)

где 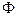– магнитный поток, сконцентрированный внутри индуктивного элемента (катушки индуктивности);

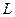– индуктивность элемента (коэффициент пропорциональности между магнитным потоком и током в индуктивном элементе), для линейного индуктивного элемента индуктивность L = const.

Подставляя в (3.26) выражение (3.25), получим:

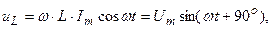(3.27)

где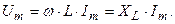

Величина 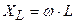называется индуктивным сопротивлением, измеряется в омах и зависит от частоты .

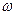Сопоставляя выражения (3.25) и (3.27), сделаем важный вывод: ток в индуктивном элементе отстает по фазе от напряжения на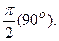

Это положение иллюстрируется на рисунке 3.5,в,г. Из формулы (3.27) следует также:

- индуктивный элемент оказывает синусоидальному (переменному) току сопротивление, модуль которого 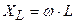прямо пропорционален частоте;

- «закон Ома» выполняется как для амплитудных значений тока и напряжения:

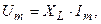(3.28)

так и для действующих значений:

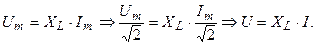(3.29)

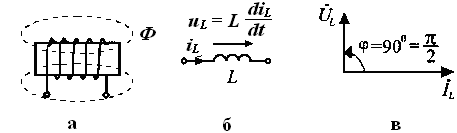
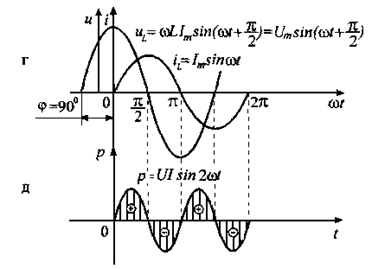
Рис. 3.5. Индуктивный элемент: а) схема конструкции катушки индуктивности;

б) изображение ИЭ на схеме; в) векторы тока и напряжения;

г) графики тока и напряжения; д) график мгновенной мощности

Выразим мгновенную мощность через i и u:

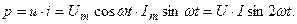(3.30)

График изменения мощности р со временем построен на основании формул (3.30) на рисунке 3.5,д. Анализ графика и (3.30) позволяют сделать выводы:

- мгновенная мощность на индуктивном элементе имеет только переменную составляющую 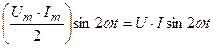, изменяющуюся с двойной частотой ( ).

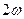- мощность периодически меняется по знаку, т.е. то положительна, то отрицательна. Это значит, что в течение одних полупериодов, когда 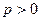, энергия запасается в индуктивном элементе (в виде энергии магнитного поля), а в течение других полупериодов, когда 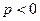, энергия возвращается в электрическую цепь.

Запасаемая в индуктивном элементе энергия за время dt равна:

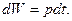(3.31)

Максимальная энергия, запасенная в индуктивном элементе, определится по формуле:

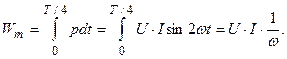(3.32)

Подставляя в (3.32) 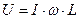, получим:

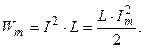(3.33)

3.2.3 Емкостный элемент. Примером емкостного элемента является плоский конденсатор – две параллельные пластины, находящиеся на небольшом расстоянии друг от друга (рис. 3.6,а).

Пусть к емкостному элементу приложено напряжение (рис. 3.6,б)

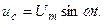(3.34)

На пластинах емкостного элемента появится заряд q, пропорциональный приложенному напряжению:

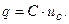(3.35)

Тогда ток в емкостном элементе

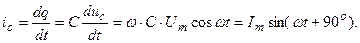(3.36)

Таким образом, получим важные соотношения:

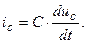(3.37)

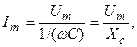(3.38)

где 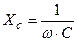– емкостное сопротивление, измеряется в омах и зависит от частоты.

Сопоставляя выражения (3.36) и (3.34), приходим к выводу: ток в емкостном элементе опережает по фазе напряжение, приложенное к нему, на 90°.

Это положение иллюстрируется на рис. 3.6,в,г.

Анализ выражений (3.36) и (3.38) позволяет сделать и другие выводы:

- емкостный элемент оказывает синусоидальному (переменному) току сопротивление, модуль которого 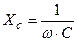обратно пропорционален частоте.

- «закон Ома» выполняется как для амплитудных значений тока и напряжения:

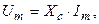(3.39)

так и для действующих значений:

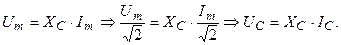(3.40)

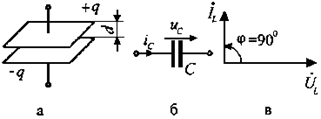
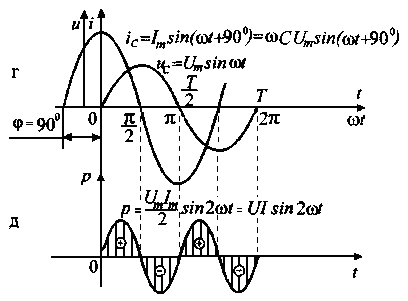
Рис. 3.6. Емкостный элемент: а) схема конструкции плоского конденсатора; б) изображение емкостного элемента на схеме; в) векторы тока и напряжения на емкостном элементе; г) графики мгновенных значений тока и напряжения;

д) график мгновенной мощности

Выразим мгновенную мощность р через i и u:

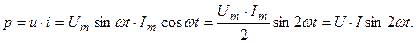(3.41)

График изменения мощности р со временем построен на рис. 3.6,д. Анализ графика и (3.41) позволяют сделать выводы:

- мгновенная мощность на емкостном элементе имеет только переменную составляющую

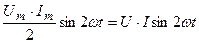, изменяющуюся с двойной частотой ( ).

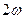- мощность периодически меняется по знаку, т.е. бывает то положительна, то отрицательна. Это значит, что в течение одних четвертей периодов, когда 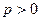, энергия запасается в емкостном элементе (в виде энергии электрического поля), а в течение других четверть периодов, когда 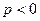, энергия возвращается в электрическую цепь.

Запасаемая в емкостном элементе энергия за время 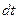равна

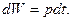(3.42)

Максимальная энергия, запасенная в емкостном элементе, определится по формуле:

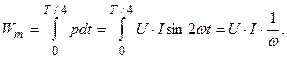(3.43)

Учитывая, что 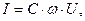получим:

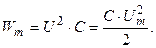(3.44)