Синусоидального тока

Для расчета режима неразветвленной электрической цепи применим комплексный метод. Представим все синусоидальные величины их комплексами:

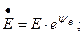
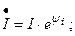
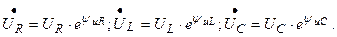
Порядок расчета такой же, как на постоянном токе. Во-первых, стрелками изображаем условные положительные направления тока, ЭДС и напряжений. Во-вторых, выбираем направление обхода контура по направлению движения часовой стрелки и записываем уравнение по второму закону Кирхгофа:

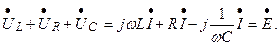(3.45)

Выражения 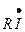, , 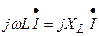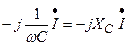отражают особенности проявления закона Ома для резистивного, индуктивного и емкостного элементов электрической цепи:

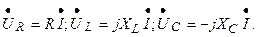
Здесь умножение на 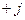означает, что напряжение 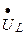опережает по фазе ток 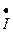на 90^º , умножение на 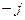означает, что напряжение 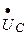отстает по фазе от тока 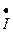на 90°.

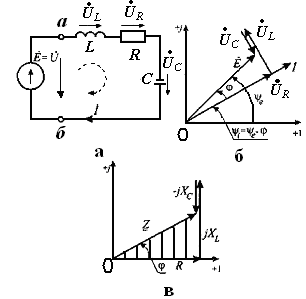
Рис. 3.7. Расчет неразветвленной электрической цепи синусоидального тока: а) схема электрической цепи; б) векторная диаграмма тока и напряжений; в) изображение комплексных сопротивлений на комплексной плоскости

Из (3.45) находим комплексный ток в цепи:

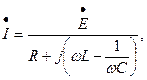(3.46)

или (так как )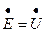

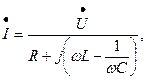(3.47)

где 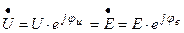– напряжение между выводами аб неразветвленной цепи (рис. 3.7,а). Величина, стоящая в знаменателе и равная

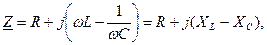(3.48)

называется комплексным сопротивлением (неразветвленной цепи).

Величина, обратная комплексному сопротивлению, называется комплексной проводимостью:

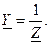
На рис. 3.7,б построена векторная диаграмма тока и напряжений неразветвленной цепи для случая: .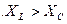

Обычно векторная диаграмма строится в конце расчета по полученным значениям тока и напряжений. При этом проверяется правильность расчета.

Поделив все составляющие векторной диаграммы на отрезок 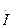, определяем значения комплексных сопротивлений и изображаем комплексные сопротивления 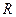, , 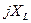, 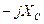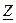на комплексной плоскости (рис. 3.7,в), тогда получаем диаграмму, подобную диаграмме тока и напряжений.

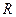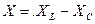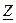Обратим внимание на «треугольник сопротивлений» (заштрихованная площадь), стороны которого соответствуют сопротивлениям , и . Треугольник сопротивлений подобен треугольнику напряжений (рис.3.7,б)

Анализ диаграммы сопротивлений позволяет перейти от алгебраической формы записи комплексного сопротивления к тригонометрической и показательной формам:

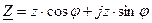; (3.49)

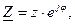(3.50)

где 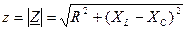– модуль комплексного сопротивления или полное сопротивление;

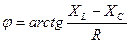– аргумент комплексного сопротивления.

В зависимости от знака величины ( 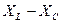) аргумент комплексного сопротивления может быть либо положительным (индуктивный характер), либо отрицательным (емкостный характер).

Подставив (3.50) в (3.46) или в (3.47), получим закон Ома для неразветвленной цепи:

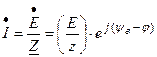(3.51)

или

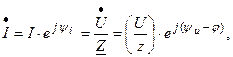(3.52)

то есть

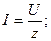
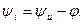(3.53)

При нескольких последовательно соединенных элементах комплексное сопротивление

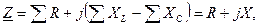(3.54)

где 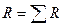– активное сопротивление цепи;

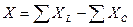– реактивное сопротивление цепи.

В активном сопротивлении происходит необратимое преобразование электрической энергии в другие виды энергии, а в реактивном сопротивлении – не происходит.

Полное сопротивление и аргумент комплексного сопротивления можно рассчитывать по формулам:

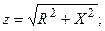(3.55)

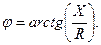(3.56)