При учёте сопротивлений линейных проводов мы вынуждены рассчитывать двухконтурную цепь с двумя узлами N- на генераторе и n - на нагрузке.

Трёхфазные цепи типа «звезда-звезда» с нулевым проводом.

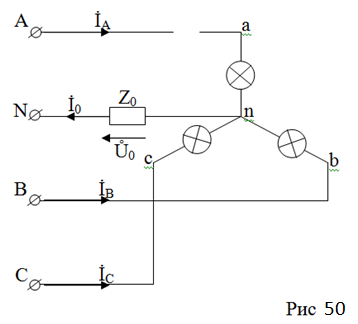
Понятно, что при обрыве фазы нагрузки или соответствующего линейного провода, например, фазы «а» и линейного провода А (рис. 50)

в цепи происходит следующее:

· лампочка в фазе «а» погаснет

· нагрузка перестает быть симметричной и появляется смещение нейтрали Ů₀= I₀z₀,вычисляемое по методу двух узлов с учётом того, что Z_a = ∞ и Y_а = 0; нейтральная точка “n” смещается вниз, увеличивая фазное напряжение U_a на величину смещения нейтрали;

· если сопротивлением нулевого провода пренебречь, в фазах «b» и «с» никаких изменений не произойдёт, нейтральная точка “n” нагрузки принудительно совместится с нейтральной точкой “N” генератора, лампочка “a” погаснет.

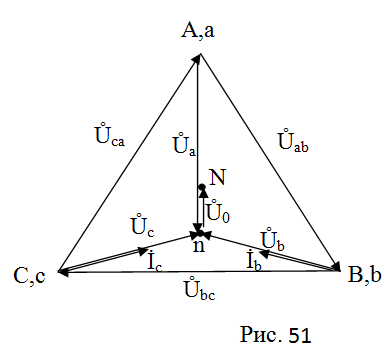
Топографическая векторная диаграмма цепи представлена на рис.51

К тяжелой ситуации в такой цепи приведёт короткое замыкание любой фазы, например фазы «а». В этом случае ток в линии А-а-n-N будет ограничиваться только незначительным по величине сопротивлением линейного провода «А» и внутренним сопротивлением источника, если они учитываются. Здесь будет иметь место резкий бросок тока, чрезвычайно опасный для работы системы.

При срабатывании защиты в линейном проводе А, сеть приводится к только что рассмотренному обрыву линии «А» (фазы «а»).

Трёхфазные цепи при соединении фаз нагрузки по схеме «треугольник».

Как и в предыдущем случае, рассмотрим вариант симметричной нагрузки в виде осветительных приборов (лампочек) одинаковой мощности, при отсутствии сопротивления в линейных проводах.

Обрыв фазы ab.

В этом случае схема цепи приобретает вид рис 52.

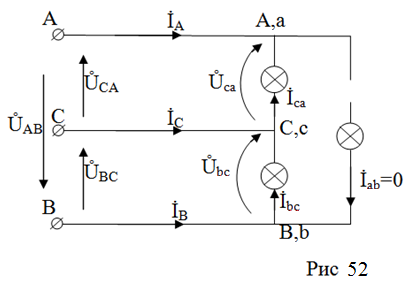
Понятно, что напряжения на нагрузке Ů_ab=Ů_AB, Ů_bc=Ů_BC, Ů_ca=Ů_CA, формируемые генератором, при любой ситуации в нагрузке остаются неизменными, сохраняя треугольник напряжений АВС=abc равносторонним. Линейные напряжения здесь равны по величине и смещенны друг относительно друга на 120°. При этом:

· ток в фазе «ab» İ_ab=0;

· ток в фазе «bc» İ_bc= ;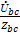

· ток в фазе «ca» İ_са= ;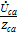

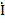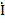· в случае одинаковых ламп накаливания (чисто активная нагрузка) фазные токи _ca и _bc совпадают по фазе с соответствующими напряжениями, равны по величине и смещены друг относительно друга по фазе на 120°;

· линейный ток İ_A оказывается равным фазному току İ_ca, но смещён относительно него по фазе на 180°;

· линейный ток İ_В равен фазному току İ_bc и совпадает с ним по фазе;

· линейный ток İ_с=İ_са-İ_bc (первый закон Кирхогофа для угла С);

· лампа в фазе «ab» погаснет;

· лампы в фазах «bc» и «СА» не изменят интенсивности горения.

Векторная диаграмма, соответствующая исследуемой цепи, представлена на рис 53.

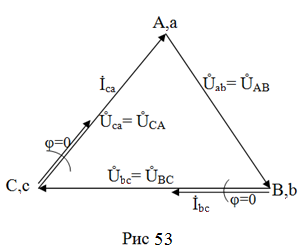
В случае, если нагрузка фаз не будет чисто активной, сдвиги по фазе между фазными токам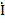и _bc и 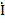_ca и напряжениями Ůbc и Ůса определяются известными соотношениями

φ_bc=arctg 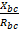и φ_ca=arctg .

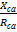В случае, если пренебречь сопротивлениями в линейных проводах невозможно, необходимо рассчитать цепь рис 54.

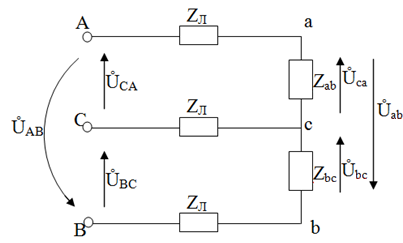
Рис 54

В этом случае Ů_ab≠Ů_AB; Ů_bc≠Ů_BC; Ů_ca≠Ů_CA, и мы имеем двухконтурную цепь, которую следует рассчитать любым известным методом расчёта сложных электрических цепей. Оптимальным будет метод двух узлов при приведении фаз генератора к «звезде» с получением нейтральной точки N.