Трёхфазные цепи при соединении фаз нагрузки по схеме «звезда» без нулевого провода.
Для простоты и наглядности анализа полагаем, что в каждую фазу включены одинаковые по мощности осветительные приборы (лампочки). Сопротивлением линии пренебрегаем. Схема и топографическая диаграмма такой цепи представлена на рис.46.
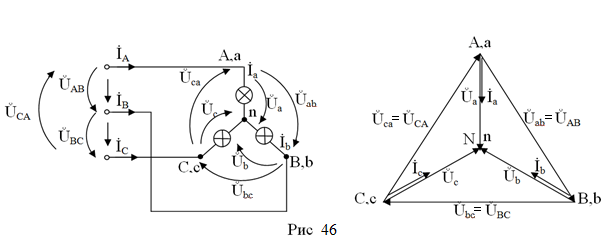
При расчёте и анализе будем исходить из того, что мощность генератора по сравнению с мощностью, потребляемой нагрузкой, бесконечна, т.е. при любых ситуациях в нагрузке линейные напряжения ŮAB=Ůab, ŮBC=Ůbc и ŮCA=Ůca остаются неизменными, а нейтральная точка на генераторене меняет своего положения, оставаясь в центре равностороннего треугольника линейных напряжений. Понятно, что сопротивление лампочек являются активными.
Обрыв фазы «а».
Обрыв фазы здесь автоматически означает обрыв соответствующей линии, в данном случае - линейного провода А (рисунок 47), что приводит к следующему:
· ток İA=İa=0 исчезает;
· лампочка в фазе «а» гаснет;
· в цепи исчезает ветвь А-а-n;
· нейтральная точка «n» на нагрузке перестаёт быть узлом (узел-место соединения минимум трёх ветвей);
· лампочки в фазах «с» и «b» теперь соединены последовательно и включены на напряжение Ůbc;
· поскольку лампочки (сопротивления) фаз «b» и «с» одинаковы, каждая из них оказывается на половине напряжения ŮBC;
· нейтральная точка нагрузки «n» перемещается на основание BC треугольника АВС;
· векторная диаграмма приобретает вид представленный на рис 47;
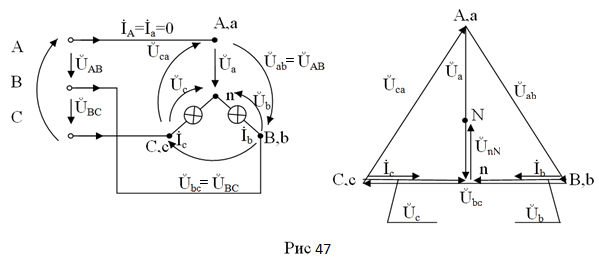
таким образом, обрыв фазы:
─ симметричную нагрузку превращает в не симметричную со смещением нейтрали ŮnN, величина которого (рассматривается геометрия равностороннего треугольника с центром в точке N) равна
UnN=  (An)= UAB·
(An)= UAB·  · cos30°=
· cos30°= 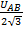 , а начальная фаза отличается от начальной фазы Ůa на 1800;
, а начальная фаза отличается от начальной фазы Ůa на 1800;
─ напряжение в фазе «a» (в разрыве фазы) возрастает на величину смещения, а в фазах «b» и «c» напряжения становятся равными половине линейного напряжения, уменьшаясь с 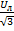 (фазные напряжения симметричной нагрузки) до
(фазные напряжения симметричной нагрузки) до  Uл;
Uл;
─ лампочка в фазе «a» погаснет, а в двух других фазах будет гореть одинаково, но с пониженной яркостью;
─ токи в фазах «b» и «c» оказываются одинаковыми по величине и равными Ib=Ic= 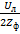 ; начальная фаза тока İс совпадает с начальной фазой линейного напряжения ŮBC, а фаза тока İb отличается от неё на 180°.
; начальная фаза тока İс совпадает с начальной фазой линейного напряжения ŮBC, а фаза тока İb отличается от неё на 180°.
Таким образом, топографическая векторная диаграмма цепи легко и понятно строится и позволяет сделать все необходимые выводы о последствиях аварии с получением новых значений электрических величин без каких-либо расчётов.
При необходимости получения точных значений электрических величин цепь должна быть рассчитана методом эквивалентных преобразований как цепь с последовательным соединением двух сопротивлений Zb и Zc, включенных на напряжение ŮBC=Ůbc. При несимметричной нагрузке нейтральная точка «n» может находиться не на середине вектора ŮBC. При Ůb≠Ůc, а треугольники abn и acn оказываются произвольными, не поддающимися простым тригонометрическим расчётам.
короткое замыканиефазы «а».
Конфигурация цепи в результате такой аварии представлена на рис 48.
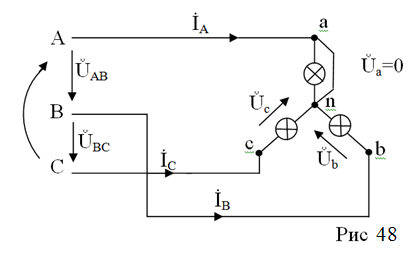
Понятно, что треугольник линейных напряжений на генераторе, а, следовательно, и на нагрузке (отсутствие сопротивлений линейных проводов) остаётся неизменным.
Короткое замыкание фазы «а» приводит к следующему:
· потенциал точки «n» в этом случае принудительно приравнивается к потенциалу точки «а» и А, что приводит к смещению нейтральной точки «n» в точку «а»;
· напряжение на фазе «а» становится равным нулю Ůa=0;
· лампочка в фазе «а» гаснет;
· напряжения фаз «b» и «с» становятся равными линейным, т.е. увеличиваются в 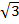 , при этом начальная фаза Ůb становится равной фазе напряжения Ůab, а фаза Ůc отличается от фазы Ůca на 180°;
, при этом начальная фаза Ůb становится равной фазе напряжения Ůab, а фаза Ůc отличается от фазы Ůca на 180°;
· лампочки фаз «b» и «с» будут гореть одинаково, но с существенно большей яркостью;
· величины токов в фазах «b» и «с» возрастают в 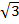 раз, совпадая по фазе с напряжением на соответствующей фазе цепи (лампочки – активная нагрузка), а ток в фазе «а» равен İа= - (İb+İc)=İА
раз, совпадая по фазе с напряжением на соответствующей фазе цепи (лампочки – активная нагрузка), а ток в фазе «а» равен İа= - (İb+İc)=İА
Векторная диаграмма напряжений и токов для этого случая представлена на рис 49.
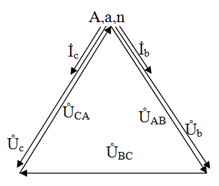
Рис 49
Понятно, что |  A|=2|
A|=2|  b|·cos30°=|
b|·cos30°=|  b|
b| 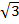 .
.
При несимметричной нагрузке и отсутствии сопротивлений в линейных проводах векторная диаграмма напряжений не изменяется, фаза «b» оказывается на напряжении Ůab, а фаза “с”- на напряжении Ůca, т.е.
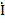 b =
b = 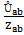 ,
, 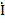 c =
c = 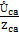 , a
, a 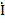 a = - (
a = - ( 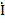 b+
b+ 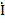 c).
c).
Сдвиг по фазе между токами определяется характером нагрузки.
Дата добавления: 2018-05-10; просмотров: 4756;











