Топографические диаграммы в трехфазных цепях
Как известно, топографическими называют такие диаграммы, каждой характерной точке которой однозначно соответствует подобная характерная точка схемы электрической цепи. Как правило, к топографическим векторным диаграммам относят диаграммы напряжений, в которых, при совмещении их с электрическими схемами совпадают и потенциалы характерных точек, и разности потенциалов между этими точками, и направления падений напряжений между ними и т.п.
Все векторные диаграммы, которые были построены в предыдущих разделах являются безупречно верными, позволяющими успешно анализировать работу цепи в любом ее режиме, но не являются топографическими.
Прежде всего потому, что направления всех векторов напряжений на этих диаграммах, по сравнению с топологией цепи изменены на противоположные.
Никаких пояснений по этому поводу нигде не дается, хотя очевидные противоречия и естественное недоумение всеми ощущается.
С тем чтобы избежать эти противоречия в некоторых случаях [ ] без каких-либо объяснений прибегают к изменению направления ЭДС фаз источника на противоположные(от начала фазы к нейтральной точке), не обращая внимания на то, что при этом нарушается весь терминологический ряд четко определенных понятий и определений, включая направление токов.
Традиционное построение векторной диаграммы трехфазной цепи начинают с построения векторов фазных напряжений и во всех случаях их строят так, как на рис. 4 и всех последующих. И здесь допускается первое и главное нарушение топологии, приводящее, в общем-то, к трудно объяснимым результатам.
Дело в том, что правила векторной алгебры приводят в этом случае к тому, что на основании второго закона Кирхгофа 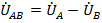 ,
, 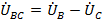 и
и 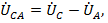 например, вектор
например, вектор 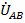 должен быть направлен не от зажима «А» генератора к зажиму «В», как на электрической схеме в соответствии с общепринятыми правилами, а от «В» к «А». То же самое происходит и с векторами
должен быть направлен не от зажима «А» генератора к зажиму «В», как на электрической схеме в соответствии с общепринятыми правилами, а от «В» к «А». То же самое происходит и с векторами 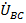 и
и 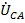 . Это приводит к тому, что в соответствии с векторной диаграммой и общепринятым правилом направления падения напряжения от точки с большим потенциалом к точке с меньшим, электрический потенциал точки «В» имеет условно большую величину, чем потенциал точки «А». Но это противоречит тому, что имеет место в реальной электрической цепи, где условна величина потенциала точки «А», конечно, больше, чем величина потенциал точки «В». Подобное относится и к потенциалам точек «В» и «С». Автоматически все это приводит к тому, что направления падений напряжений в линейных проводах, в нулевом проводе, в принципе, между любыми двумя токами в электрической цепи и на векторной диаграмме направлены в противоположные стороны. Чтобы исключить эти недоразумения в некоторых случаях [1] прибегают к изменению на противоположные направлений токов и падений напряжений в исходной схеме, что, по сути, приводит к еще большим недоразумениям.
. Это приводит к тому, что в соответствии с векторной диаграммой и общепринятым правилом направления падения напряжения от точки с большим потенциалом к точке с меньшим, электрический потенциал точки «В» имеет условно большую величину, чем потенциал точки «А». Но это противоречит тому, что имеет место в реальной электрической цепи, где условна величина потенциала точки «А», конечно, больше, чем величина потенциал точки «В». Подобное относится и к потенциалам точек «В» и «С». Автоматически все это приводит к тому, что направления падений напряжений в линейных проводах, в нулевом проводе, в принципе, между любыми двумя токами в электрической цепи и на векторной диаграмме направлены в противоположные стороны. Чтобы исключить эти недоразумения в некоторых случаях [1] прибегают к изменению на противоположные направлений токов и падений напряжений в исходной схеме, что, по сути, приводит к еще большим недоразумениям.
В то же время недоразумение легко устраняется, если обратиться к опорным векторам. Дело в том, что по повсеместно принятому определению фазные напряжения на генераторе 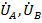 ,
,  как падения напряжения на фазах генератора направлены не от нейтральной точки «N» к началу фаз А, В и С, а в обратную сторону, фиксируя очевидное соотношение между условными величинами потенциалов этих точек. Таким образом, на топографических диаграммах векторы
как падения напряжения на фазах генератора направлены не от нейтральной точки «N» к началу фаз А, В и С, а в обратную сторону, фиксируя очевидное соотношение между условными величинами потенциалов этих точек. Таким образом, на топографических диаграммах векторы 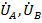 и
и  должны быть направлены так, как показано на рис. 38.
должны быть направлены так, как показано на рис. 38.
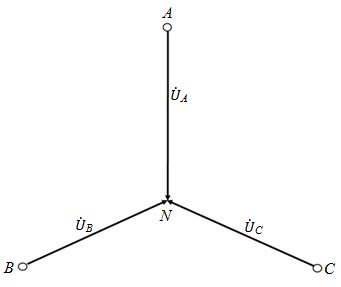
Рис. 38
Совершенно ясно, что соотношение между 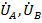 и
и  по фазам здесь остается прежним (120°) с сохранением прямого чередования фаз А-В-С, в чем легко убедиться, построив эти векторы параллельным переносом из одной точки.
по фазам здесь остается прежним (120°) с сохранением прямого чередования фаз А-В-С, в чем легко убедиться, построив эти векторы параллельным переносом из одной точки.
Если векторы фазных напряжений как опорных для построения топографической векторной диаграммы построить именно так, все остальные векторы занимают свои места в соответствии с топологией цепи. Полная топографическая диаграмма приобретает законченный логически безупречный вид, с полным соответствием всех точек цепи аналогичным точкам диаграммы и с четким соответствием направлений падений напряжений на схеме с направлением векторов на диаграмме (рис. 39).
Здесь 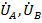 и
и  - фазные напряжения на генераторе, в соответствии с принятыми правилами направленные от начал фаз генератора А, В и С к нулевой (нейтральной) точке N с полным соответствием между точками А, В, С и N на схеме и топографической диаграмме.
- фазные напряжения на генераторе, в соответствии с принятыми правилами направленные от начал фаз генератора А, В и С к нулевой (нейтральной) точке N с полным соответствием между точками А, В, С и N на схеме и топографической диаграмме.
Векторы линейных напряжений на генераторе 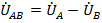 ,
, 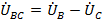 и
и 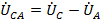 образуют при этом равносторонний (симметричная система ЭДС) треугольник и направлены соответственно от А к В, от В к С и от С к А. поскольку рассматривается общий случай несимметричной нагрузки, нейтральные точки нагрузки «n» и генератора «N» смещаются друг относительно друга на величину смещения нейтрали
образуют при этом равносторонний (симметричная система ЭДС) треугольник и направлены соответственно от А к В, от В к С и от С к А. поскольку рассматривается общий случай несимметричной нагрузки, нейтральные точки нагрузки «n» и генератора «N» смещаются друг относительно друга на величину смещения нейтрали 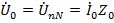 с направлением вектора
с направлением вектора 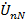 от «n» к «N», как и на схеме.
от «n» к «N», как и на схеме.
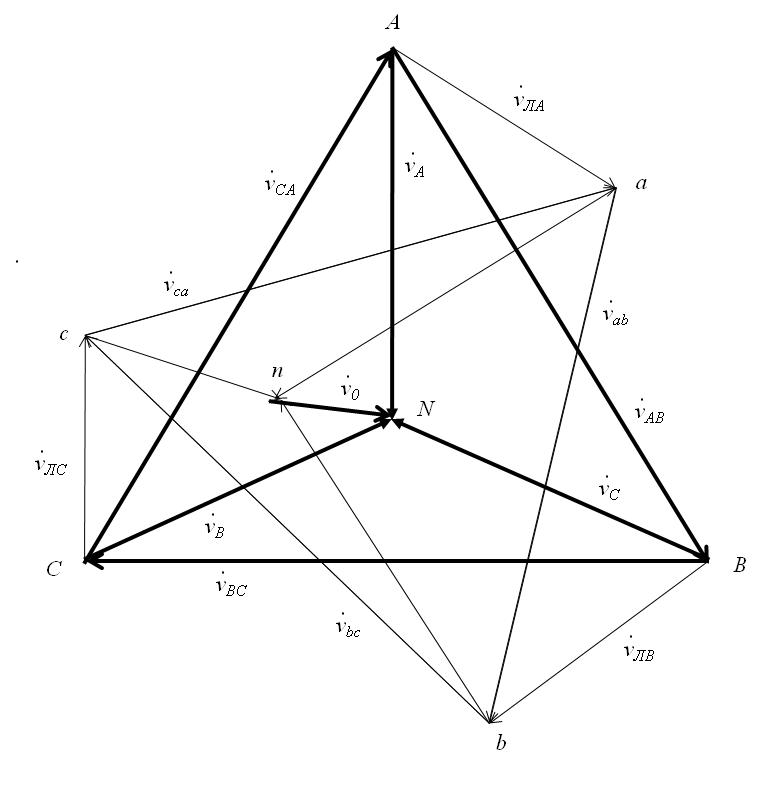
Рис. 39
При наличии сопротивлений в линейных проводах в них возникают падения напряжения 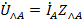 ,
, 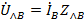 ,
, 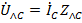 направленные по направлению тока от начал фаз А, В и С на генераторе к началам фаз a, b и c на нагрузке (смещение начал фаз).
направленные по направлению тока от начал фаз А, В и С на генераторе к началам фаз a, b и c на нагрузке (смещение начал фаз).
Это приводит к искажению линейных напряжений (несимметричная нагрузка) на фазах нагрузки. Треугольник линейных напряжений на нагрузке «abc» оказывается произвольным со сторонами, представляющими векторы линейных напряжений на нагрузке 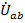 ,
, 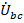 и
и 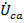 с соответствующими направлениями от «a» к «b», от «b» к «c», «c» к «a».
с соответствующими направлениями от «a» к «b», от «b» к «c», «c» к «a».
Фазные напряжения на нагрузке, как и положено, представлены векторами 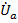 ,
, 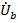 и
и 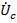 , направленными (как на схеме) соответственно от точек a, b и c к нулевой точке нагрузки «n».
, направленными (как на схеме) соответственно от точек a, b и c к нулевой точке нагрузки «n».
При понимании всего этого никаких проблем с построением векторных диаграмм для цепи любой конфигурации вообще возникать не будет, ибо каждой точке цепи соответствует конкретная точка на диаграмме с четким определением направления векторов. При этом второму закону Кирхгофа, лежащему в основе построения векторных диаграмм напряжений, для любого замкнутого контура в цепи точно соответствует конкретная фигура, составленная из соответствующих векторов векторной диаграммы с соблюдением их знаков. Например, второй закон Кирхгофа для контура N-A-a-n-N схемы электрической цепи имеет вид: 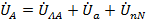 . На векторной диаграмме это уравнение представлено соответствующей этим точкам (буквам) фигурой N-A-a-n-N, представляющей векторы
. На векторной диаграмме это уравнение представлено соответствующей этим точкам (буквам) фигурой N-A-a-n-N, представляющей векторы 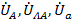 и
и 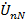 , обход которой по этим векторам приводит к
, обход которой по этим векторам приводит к 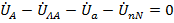 , т.е.
, т.е. 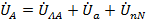 .
.
Конечно, топографическая векторная диаграмма трехфазной цепи оказывается более точной, более информативной и понятной при ее построении и использовании для анализа цепи.
Однако с тем, чтобы не создавать трудности изучающим трехфазные цепи с использованием разных источников(учебников), все векторные диаграммы в настоящем пособии строятся с традиционно сложившимся нарушением принципов топологии, что несколько затрудняет понимание, но не приводит к каким-либо принципиальным ошибкам.
Дата добавления: 2018-05-10; просмотров: 5150;











