Определение мощности через симметричные составляющие
Как уже было отмечено, в основе симметричных составляющих лежит принцип наложения. Заданный несимметричный режим работы трехфазной цепи представляется как результат наложения трех симметричных режимов. Применение метода симметричных составляющих базируется на независимости действия симметричных составляющих в трехфазной цепи, т.е. на фундаментальном принципе независимости действия сил в линейных системах.
Это значит, что применение этого метода ограничивается только линейными трёхфазными цепями, либо с соблюдением условий приведения нелинейных цепей к эквивалентным линейным.
Последовательность традиционного варианта расчёта для случая несимметричной системы напряжений состоит в следующем:
1. Заданная несимметричная система питающих напряжений  A,
A,  B и
B и  C по правилам,
C по правилам,
изложенным в п. 4.1, разлагается на три симметричные составляющие:
- систему с прямым чередованием фаз, в которой
 A1 =
A1 = 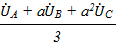 ,
,  B1 =
B1 =  A1e-j120º и
A1e-j120º и  C1 =
C1 =  A1e-j240º;
A1e-j240º;
- систему с обратным чередованием фаз, в которой
 A2 =
A2 = 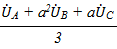 ,
,  B2 =
B2 =  A2e-j240º, а
A2e-j240º, а  C2 =
C2 =  A2e-j120º.
A2e-j120º.
- Систему нулевой последовательности, для которой  A0 =
A0 =  B0 =
B0 =  C0 =
C0 = 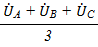 .
.
2. С учётом принципа независимости действия сил производится расчёт исследуемой
трёхфазной цепи на каждой из составляющих систем напряжения. Понятно, что никакого влияния каждая из трёх симметричных систем при расчёте друг на друга не оказывают.
Цепи рассчитываются на основе известных методов расчёта трёхфазных цепей с соблюдением чередования фаз.
Конечно, расчёт цепи с нулевым чередованием фаз имеет свои особенности, почти полностью приводящие трёхфазную цепь к обычной сложной цепи переменного тока с потерей ряда относящихся к трёхфазным цепям зависимостей и одновременным приобретением ряда новых, включая изложенные в п. 4.1.
3. Реальные токи и напряжения на отдельных элементах исходной трёхфазной цепи определяются наложением друг на друга частных симметричных режимов. Например, реальные токи в линейных проводах:
 A =
A =  A0 +
A0 +  A1 +
A1 +  A2,
A2,
 B =
B =  B0 +
B0 +  B1 +
B1 +  B2,
B2,
 C =
C =  C0 +
C0 +  C1 +
C1 +  C2.
C2.
Понятно, что при симметричных нагрузках
 A0 =
A0 =  B0 =
B0 =  C0
C0
 B1 = а2
B1 = а2  A1 и
A1 и  C1 = а
C1 = а  A1, т.е. как и во всех предыдущих случаях расчёт может быть произведён только для одной фазы.
A1, т.е. как и во всех предыдущих случаях расчёт может быть произведён только для одной фазы.
Конечно, при расчёте трехфазных цепей следует учитывать некоторые связанные с этим методом особенности. Кроме того, о чём было сказано в п. 4.1 необходимо иметь в виду следующее. Следует понимать, что сопротивления отдельных участков цепи для фазного чередования фаз могут оказаться разными.
Например, для трёхфазных цепей со статическими нагрузками, т.е. такими, в составе которых отсутствуют вращающиеся элементы (асинхронные и синхронные машины с вращающимися роторами) сопротивления для прямого и обратного чередования фаз будут одинаковыми. Однако, в случае присутствия в напряжении нулевой последовательности на величину сопротивления элементов влияет схема их соединения.
Например, легко видеть, что в случае соединения симметричной нагрузки (zA = zB = zC = z) по схеме «звезда» сопротивления фаз и нулевого провода для прямого и обратного чередования фаз будут одинаковыми (рис. 59).
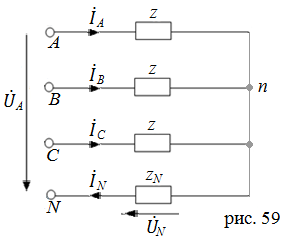
Однако для системы нулевой последовательности сопротивления нулевого оказывается иным, в чём легко убедиться, составив уравнение по второму закону Кирхгофа, например, для контура A – n – N – A этой цепи:
 A =
A =  AZ +
AZ +  NZN.
NZN.
Учитывая, что  A =
A =  B =
B =  C =
C =  0 и то, что в этом случае
0 и то, что в этом случае
 N0 =
N0 =  A0 +
A0 +  B0 +
B0 +  C0 = 3
C0 = 3  0, получаем
0, получаем
 A0 =
A0 =  A0Z +
A0Z +  N0ZN =
N0ZN =  0Z + 3
0Z + 3  N0ZN =
N0ZN =  0(Z + 3ZN) =
0(Z + 3ZN) =  NZN0, что означает, что сопротивление нулевого провода для нулевого чередования фаз фактически больше ZN и равно ZN0 = Z + 3ZN.
NZN0, что означает, что сопротивление нулевого провода для нулевого чередования фаз фактически больше ZN и равно ZN0 = Z + 3ZN.
С точки зрения теории цепей здесь нет ничего необычного, поскольку фактически в составе тока нулевого провода в этом случае параллельно действуют три одинаковых тока каждой фазы  A0,
A0,  B0 и
B0 и  C0. Эти токи на сопротивлении нулевого провода формируют три одинаковых падения напряжения, т.е.
C0. Эти токи на сопротивлении нулевого провода формируют три одинаковых падения напряжения, т.е.  N0 = (
N0 = (  A0 +
A0 +  B0 +
B0 +  C0)ZN = 3
C0)ZN = 3  0ZN.
0ZN.
Если нулевой провод отсутствует, то ZN = ∞ и  N0 = 0.
N0 = 0.
В случае присутствия в цепи электрических машин с вращающимся ротором сопротивления этих машин для нулевой, прямой и обратной последовательностей оказываются существенно разными в связи с тем, что индуцируемые магнитными полями в обмотках машин зависящие от частоты индуктивные сопротивления отличаются друг от друга, поскольку частота индуцируемых в обмотках ЭДС при обратном чередовании фаз становится равной удвоенной частоты питающего напряжения (прямого чередования фаз), при этом следует помнить, что частота ЭДС и токов в роторе отличается от частоты статора с учётом величины скольжения. Во всех случаях Ф1 > Ф2, Х1 > Х2, Z1> Z2.
Что касается особенностей собственно метода расчёта, следует обратить внимание на то, что в ряде случаев при расчёте трёхфазных систем с присутствием в них несимметричной нагрузки значительной мощности, оказывается целесообразным несимметричные сопротивления в фазах заменять падением напряжений на них с разложением получаемой таким образом системы несимметричных напряжений на симметричные составляющие прямой, обратной и нулевой последовательностей. При этом цепь рассчитывается на каждой из них с учётом лишь того, что симметричная система ЭДС генератора содержит только симметричные составляющие с прямым чередованием фаз. Неизвестными в этом случае являются напряжения на несимметричной нагрузке. После их вычисления легко вычислить все токи в рассматриваемой цепи.
Дата добавления: 2018-05-10; просмотров: 1333;











