Дифференциальные уравнения САУ

Анализ САУ

Тенденция к усложнению структуры САУ и выполняемых ими функций увеличивает трудности исследования их статики и динамики и повышает значение правильного подхода к выбору методов исследования. В частности, наладочные работы с САУ, выполняемые интуитивно, методом проб и ошибок, подбором параметров настройки автоматических регуляторов, занимает много времени. Примером может служить настройка одноконтурной САР с ПИ-регулятором. Диапазон настройки коэффициента пропорциональной составляющей К_п = 1 – 10, а коэффициент настройки времени интегрирования Т_и = 0,5 – 200 с. Если методом подбора устанавливать К_р через два деления (ΔК_р = 2), а время интегрирования через 5 с (ΔТ_и = 5 с), то при взаимозависимых параметрах настройки регулятора для нахождения приемлемых значений надо перебрать 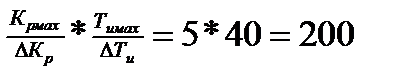сочетаний параметров.

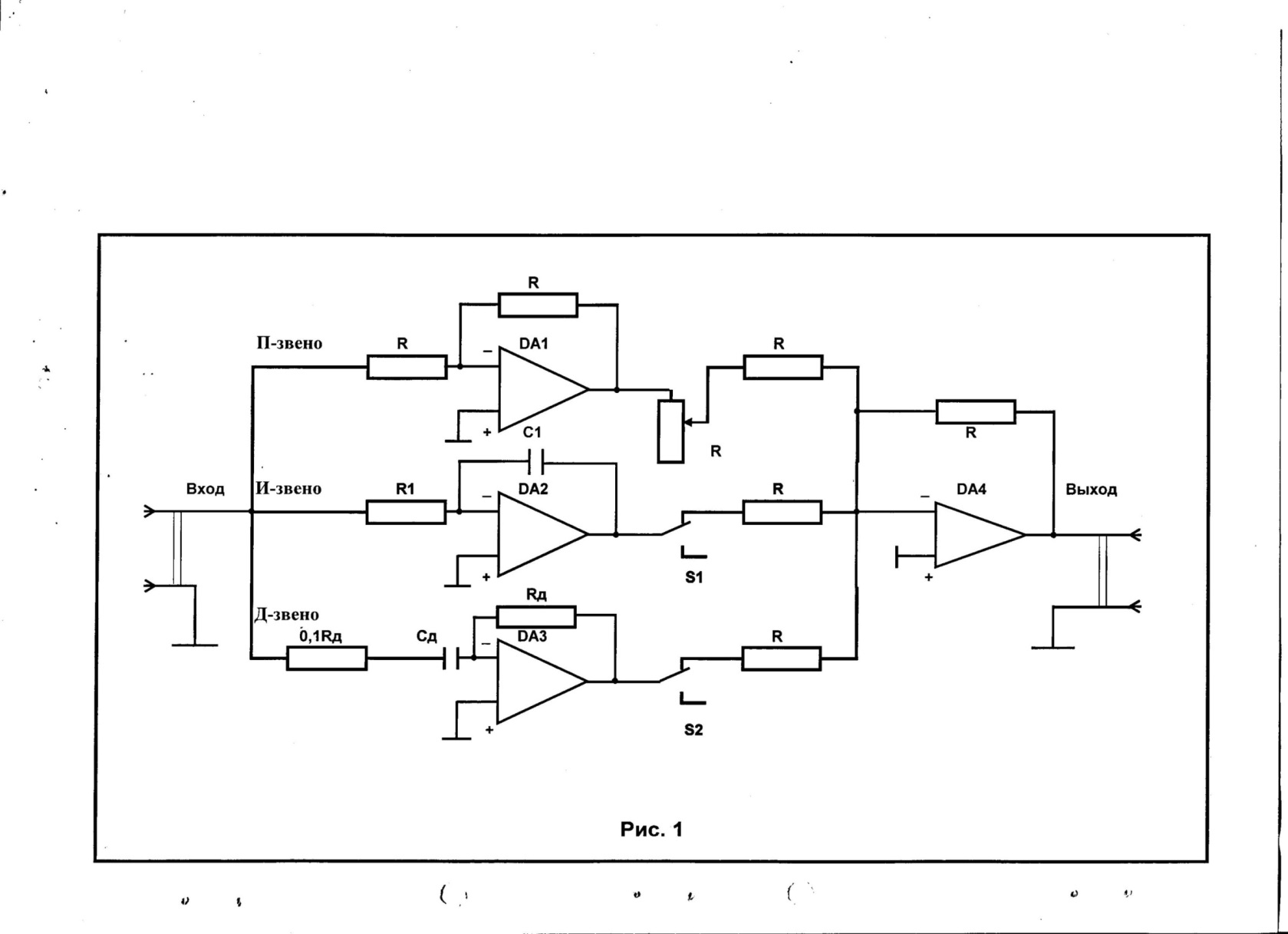
Если ОУ имеет даже относительно небольшую инерционность и его время регулирования равно, например, 1 мин, то для опробования системы при всех сочетаниях потребуется 200 сек = 3,3 часа. Если необходимо настроить многоконтурную САУ с несколькими регуляторами, то число сочетаний возрастает многократно. Имея определенный опыт, наладчик сразу определит необходимый диапазон изменения параметров регуляторов. Но не каждый технологический объект управления допускает пробные раскачки.

Целью исследования САУ может быть решение одной из двух задач: анализа или синтеза.

В первом случае дается система, включая значения параметров, и требуется определить ее свойства.

Во втором случае, наоборот задаются свойства, которыми должна обладать система, т.е. требования к ней, и необходимо создать систему, удовлетворяющую этим требованиям.

В самом общем виде порядок исследования САУ в обоих случаях включает математическое описание системы, исследование ее в установившихся режимах и исследование переходных режимов.

Математическое описание может быть выполнено аналитическим (с помощью уравнений), графическим (с помощью графиков, структурных схем и графов) и табличным (с помощью таблиц).

Для получения математического описания системы обычно составляют описание ее отдельных элементов. В частности, для получения уравнений системы составляют уравнения для каждого входящего в нее элемента. При этом систему разбивают на возможно более простые звенья, но вместе с тем необходимо, чтобы они обладали направленностью действия, т.е. чтобы влияние последующего звена на состояние предыдущего было как можно меньше. В результате этого математическое описание каждого такого звена может быть составлено без учета связей его с другими звеньями. Соответственно, математическое описание всей системы в целом может быть получено как совокупность составленных независимо друг от друга отдельных звеньев, образующих систему, и дополненных уравнениями связи между ними.

Уравнения (а также структурные схемы) САУ называют ее математической моделью. Математическая модель одной и той же системы в зависимости от цели исследования может быть разной.

Система автоматического управления и любой ее элемент производят преобразование входного сигнала X(t) в выходной сигнал Y(t). С математической точки зрения они осуществляют отображение, 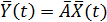согласно которому каждому элементу 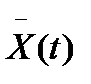из множества 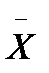входных сигналов 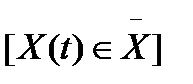ставится в соответствие единственный вполне определенный элемент Y(t) из множества 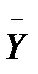выходных сигналов .

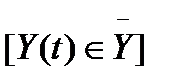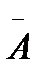- оператор системы (элемента).

Задать оператор – значит задать правила определения выходного сигнала этой системы по ее входному сигналу.

В теории и практике исследования САУ наибольшее распространение получили следующие формы математических моделей элементов и систем:

- каноническая форма записи дифференциальных уравнений;

- запись в форме пространства состояния;

- передаточные функции;

- частотные функции;

- временные функции.

Дифференциальные уравнения САУ

Составление дифференциальных уравнений начинается с составления дифференциальных уравнений ее звеньев на основе физических законов, описывающих процессы, которые в них протекают. Этот этап анализа системы является наиболее важным, поскольку неточности в исходных предпосылках, допустимой степени идеализации может свести на нет все последующие результаты. Существующие судовые САУ

в общем случае представляют собой нелинейные системы и описываются уравнениями вида

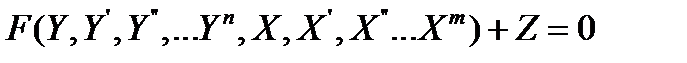, где всегда n > m

Уравнения, описывающее процессы в САУ или звене при произвольных входных воздействиях, называют уравнениями динамики.

Если входные воздействия постоянны, 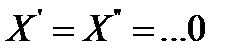, X = const и Z = const, то с течением времени процессы в САУ или звене установятся и выходная величина примет постоянное значение 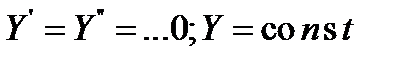, Тогда уравнение примет вид

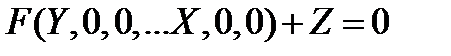. Это уравнение описывает статический или установившийся режим и его называют уравнением статики.

Статический режим можно описать графически с помощью статических характеристик. Статической характеристикой называют зависимость выходной величины Y от входной величины X в статическом режиме. Она может быть снята экспериментальным путем или расчетным путем, используя уравнения статики.

Если звено или САУ имеют несколько входов, то они описываются с помощью семейства статических характеристик.

В лабораторных работах снимались статические характеристики некоторых звеньев (генераторов, двигателей и т.д.), как зависимости выходных величин от управляющих и возмущающих величин.

Рассмотрим для примера САР частоты вращения ЭД постоянного тока.

Электродвигатель постоянного тока описывается следующими уравнениями:

- якорной цепи;

- ЭДС вращения;

- характеристики намагничивания;

- обмотки возбуждения;

- равновесия моментов вращения и сопротивления

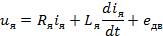
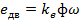
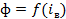
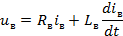
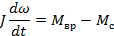
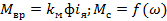
Предполагая, что частота вращения двигателя 𝜔 регулируется путем изменения напряжения якоря u_я, и, следовательно, Ф = const, уравнение моментов решим относительно тока якоря:

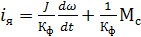, где К_ф = k_м Ф

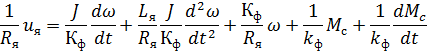
После преобразований, получим

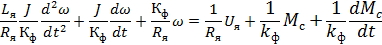
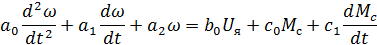
где ; ;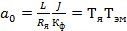

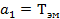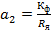
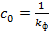
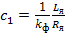
Если в математическое описание двигателя включить обмотку возбуждения, то необходимо учитывать нелинейность характеристики намагничивания.

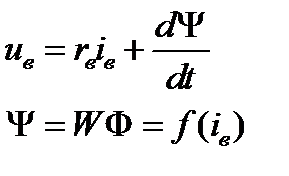
Уравнение тиристорного преобразователя (управляемого выпрямителя), работающего в режиме непрерывного тока, упрощенно можно записать так:

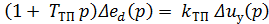(4)

где T_ТП = τ +T_ф - эквивалентная постоянная времени тиристорного преобразователя;

T_ф - постоянная времени фильтра;

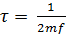- среднестатистическое запаздывание преобразователя, связанное с числом фаз сети m и частотой f;

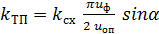- коэффициент передачи ТП по управлению (рис.5).

Для системы управления, имеющей пилообразную форму опорного напряжения с максимальным опорным напряжением 12 В, и мостовой трехфазной схемы ТП

k_ТП = 39,1 sinα