Теплоёмкость газов. Зависимость теплоёмкости от температуры и процесса. Истинная и средняя теплоёмкость.

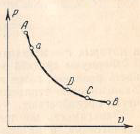
В термодинамике значительную роль играет понятие теплоёмкости газа. Рассмотрим процесс AB, в котором при сообщении 1 кг газа теплоты q его температура возрастает от T1 до T2. Отношение теплоты q к изменению температуры T2- T1 называется теплоёмкостью газа: (рис.4) → → → → → → 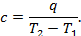Как видно, теплоёмкость это количество теплоты, необходимое для повышения температуры 1 кг газа на 1оС. Теплоёмкость газа есть переменная

величина, если её определять на различных участках AB, AC, AD процесса AB, то 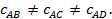Это показывает, что на отдельных участках процесса, на которых температура изменяется на 1^оС, расходуются различные количества теплоты. Поэтому приведённая выше формула не определяет действительный удельный расход теплоты, а показывает лишь, сколько теплоты в среднем в процессе AB сообщается при нагревании газа на 1^оС.

Средняя теплоёмкость – отношение теплоты, сообщаемой газу, к изменению его температуры при условии, что разность температур является конечной величиной. Под истинной теплоёмкостью газа понимают предел, к которому стремится средняя теплоёмкость при стремлении ΔT к нулю. Так, если в процессе Aa средняя теплоёмкость 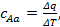то истинная теплоёмкость при начальном состоянии A:

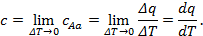
Следовательно, истинной теплоёмкостью называется отношение теплоты, сообщаемой газу в процессе, к изменению его температуры при условии, что разность температур исчезающее мала.

Общие формулы теплоты. Из приведённых выше формул следует, что теплоту, сообщаемую газу в произвольном процессе, можно определить по формуле:

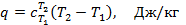
или для произвольного количества газа

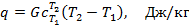
где 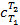– средняя теплоёмкость газа в рассматриваемом процессе при измене6нии его температуры от T₁ до T₂. Теплоту можно определить также по формулам:

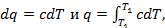где c – истинная теплоёмкость газа.

Формулы средней и истинной теплоёмкости. Теплоёмкость реальных газов зависит от давления и температуры. Зависимостью от давления часто пренебрегают. Зависимость от температуры значительна и на основании экспериментальных данных выражается уравнением вида 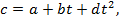где a, b, d – числовые коэффициенты, зависящие от природы газа и характера процесса.

Удельные теплоёмкости:

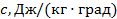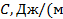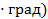Теплоёмкость, отнесённая к 1 кг газа, называется весовой теплоёмкостью – . Теплоёмкость, отнесённая к 1 м³ газа, называется объёмной теплоёмкостью – ³ . Теплоёмкость, отнесённая к 1 молю газа, называется мольной теплоёмкостью – .

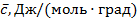Пусть для нагревания 1 кг газа на 1^оС необходимо 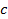джоулей тепла. Т.к. в моле содержится 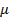килограмм газа, то для нагревания 1 моля на 1^оС необходимо в 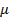раз больше тепла, т.е.

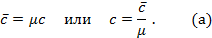
Теперь для нагревания 1 м³ газа на 1^оС необходимо 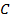джоулей тепла. Т.к. в моле при нормальных условиях содержится 22,4 м³ газа, то для нагревания 1 моля на 1^о необходимо в 22,4 раза больше, тепла:

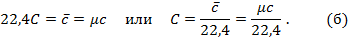
Сравнивая формулы (а) и (б), найдём зависимость между весовой и объёмной теплоёмкостями:

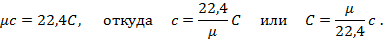
Зависимость теплоёмкости от характера процесса. Рассмотрим два процесса подвода тепла к газу:

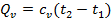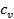а) Тепло подводится к 1 кг газа, заключённому в цилиндр с неподвижным поршнем (рис.5). Тепло, сообщённое газу, будет равно , где – теплоёмкость газа пр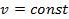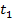и ; и 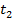– начальная и конечная температуры газа 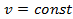. При разнице температур 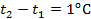получим, что 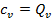. Очевидно, что всё тепло в этом случае пойдёт на увеличение внутренней энергии газа.

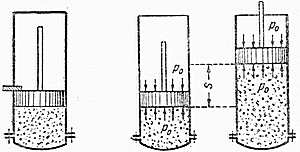
Рис. 5. Рис. 6.

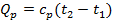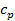б) Тепло подводится к 1 кг газа, заключённому в цилиндр с подвижным поршнем (рис.6) и, в этом случае, будет равно , где – теплоёмкость газа пр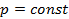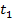и ; и 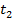– начальная и конечная температуры газа 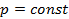при . При 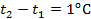получим, что 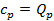. В этом случае подведённое к газу тепло пошло на на увеличение внутренней энергии газа (как и в первом случае), а также на совершение работы при движении поршня. Следовательно, для повышения температуры 1 кг газа на 1^оС во втором случае необходимо больше теплоты, чем в первом, т.е. .

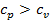Рассматривая другие процессы, можно установить, что теплоёмкость может принимать самые разные числовые значения, т.к. количество теплоты, сообщаемое газу, зависит от характера процесса.

Связь между 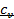и 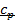, коэффициент 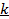. При нагревании 1 кг газа на 1^оС при 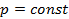подводится 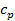Дж тепла. Часть его, равная 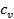, идёт на увеличение внутренней энергии, а часть – на совершение работы расширения. Обозначим эту работу через 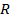. Т.к. теплота, затраченная на нагревание газа и совершение работы, должна быть в сумме равна подведённой теплоте, то можно записать, что

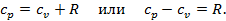
Можно показать, что величина 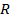есть газовая постоянна в уравнении состояния газа .

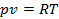В термодинамике часто используется отношение теплоёмкости при постоянном давлении к теплоёмкости при постоянном объёме

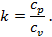
Для идеальных газов 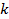– величина постоянная и зависит от природы газа (от его атомности). В таблице приведены теоретические значения теплоёмкостей согласно молекулярно-кинетической теории.

Число атомов в молекуле
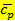
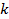
	2,98	4,96	1,67
	4,97	6,97	1,4
	5,96	7,96	1,33

Лекция 3. Первый закон термодинамики (всё тот же)