Прогрессивная деформация. Связь напряжения с деформацией

Конечная деформация, в результате которой первоначальная материальная сфера принимает форму эллипсоида (эллипсоид конечных деформаций), накапливается в ходе последовательных приращений деформации (см. разд. 8.2), т. е. в процессе так называемой прогрессивной деформации.

При очень малом начальном приращении форма эллипсоида деформаций слабо отличается от сферической, хотя и направления его главных осей могут изменяться. Если оси эллипсоидов деформаций малых приращений при прогрессивной деформации сохраняют свои направления, то деформация называется соосной или коаксиальной (например, в случае чистой деформации и чистого сдвига при плоской деформации . К = 1) (рис. 2. 17, а).

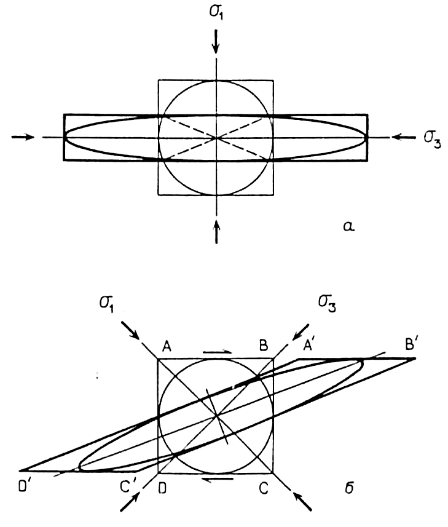
Рис. 2. 17. Типы деформации и соотношения напряжение-деформация (проекция на плоскость, перпендикулярную осям ơ₂ и Y). А - соосная деформация (чистый сдвиг): пунктиром показаны инвариантные плоскости; б - несоосная деформация

Если же параллельность осей не сохраняется, то прогрессивная деформация является несоосной. Так, при плоской сдвиговой деформации, изображенной на рис. 2. 17, 6 (ось Y не меняется), оси X и Z эллипсов добавочных деформаций неизменно ориентированы под 45° к плоскости сдвига, но соответствующие оси эллипса прогрессивной деформации постепенно поворачиваются таким образом. что ось X стремится к направлению AB.

Этот тип деформации называется простым сдвигом. В нем плоскости сдвига (параллельные AB и CD на рис. 2. 17, 6) не испытывают деформации, т. е. инвариантны. В случае чистого сдвига (при плоской деформации) имеются две инвариантные плоскости, определяемые пересечением первоначальной материальной сферы с эллипсоидом конечных деформаций (рис. 2. 17, а). В процессе прогрессивной деформации эти плоскости поворачиваются. Чистая деформация и простой сдвиг-два главных типа деформации. В тектонических процессах они могут проявляться одновременно или по отдельности.

Рассматривая рис. 2, 17, а и б, мы видим, что геометрически подобные эллипсы можно получить из деформаций чистого и простого сдвигов. С позиций конечной деформации мы имеем право считать простой сдвиг идентичным чистому сдвигу с последующим наложенным на него вращением. Это правило имеет силу лишь постольку, поскольку рассматривается переход от начального прямо в конечное состояние.

На самом же деле к процессу прогрессивной деформации оно не применимо. Чистую деформацию и простой сдвиг можно различить, когда путь деформации удается проследить по имеющимся индикаторам (см. пунктирные кривые на рис. 2.1) или известна преимущественная ориентировка кристаллографических осей при пластической деформации (разд. 7.5).

Связь напряжения с деформацией. Здесь мы ограничимся двумя типами деформаций, рассмотренными в разд. 2.4, для которых допускается плоская деформация (ось Y эллипсоида деформации неизменна и параллельна оси напряжения ơ₂) и изотропность реологических свойств.

При деформации соосного типа (чистая деформация) оси X, Y и Z эллипсоида прогрессивной деформации совпадают с главными осями напряжений ơ₃, ơ₂ и ơ₁ соответственно. Кубик, выделенный в первоначальном материале, с гранями, перпендикулярными этим направлениям, деформируется так, что грани испытывают параллельный перенос и на них действуют только нормальные напряжения.

В отличие от этого при несоосной деформации, такой, как простой сдвиг (рис. 2. 17, б), оси X и Z эллипсоида прогрессивной деформации поворачиваются относительно фиксированных осей ơ₃ и ơ₁. Поэтому здесь аналогичный кубик подвергается сдвиговому и нормальному напряжениям. Максимального значения касательные напряжения достигают на гранях куба ABCD, наклоненных под углом 45° к осям ơ₁ и ơ₃

В случае известных напряжений тип деформации контролируется анизотропными свойствами материала, например сланцеватостью, и (или) наличием границ, например близостью к стенкам для материала, залегающего в трещинах. В примере, приведенном на рис. 2. 17, 6, эти условия вызывают скольжение вдоль плоскостей, параллельных AB, но не AD.