Огибающая Мора и критерий Кулона. Парциальное давление флюида и эффективное давление

При помощи графика, показанного на рис. 3.2, и диаграммы Мора (рис. 2.16) можно вычислить сдвиговое напряжение тс, при котором достигается точка разрушения материала с ростом всестороннего давления. Дальнейший анализ, строго говоря, справедлив для изотропного материала, например такого, в котором нет кливажа, создающего предпочтительные плоскости разрывов. Экспериментальная кривая разрушения определяет зависимость максимального сопротивления материала 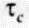от всестороннего давления. Эта кривая, называемая огибающей Мора, дает максимальное напряжение сдвига, поддерживаемое материалом в момент разрушения (рис. 3.4).

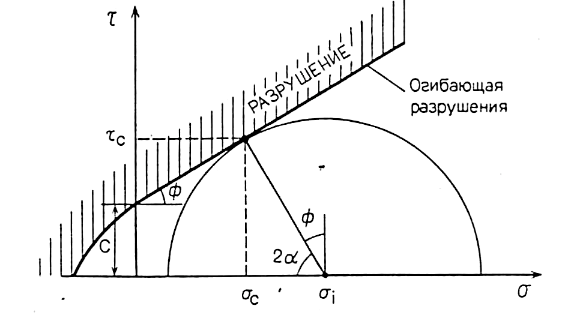
Рис. 3.4. Критерий разрушения на диаграмме Мора

Координаты точки касания позволяют найти максимальные нормальное ơ_с и сдвиговое т_с напряжения, которые действуют на плоскость разрыва при данном всестороннем давлении. Из этой же диаграммы устанавливается положение плоскости разрыва, т. е. угол ее наклона а к направлению ơ₁.

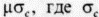В области сдвигового разрушения при умеренном всестороннем давлении эта огибающая представляет собой прямую линию, характеризующую критерий Кулона . Согласно этому критерию, сопротивление сдвигу складывается из постоянного напряжения С, описывающего сцепление частиц, и произведения - нормальное напряжение в момент разрушения и µ - коэффициент внутреннего трения.

После того как разрушение началось, смещение вдоль плоскости сдвига зависит от шероховатости контактирующих поверхностей с коэффициентом трения µ. Из рис. 3.4 видно, что С представляет собой максимальное касательное напряжение в неразрушенном материале при атмосферном давлении, а величина µ = tg ȹ определяет наклон кривой разрушения к горизонтальной оси. Угол ȹ называется углом внутреннего трения и на диаграмме Мора является также дополнительным к углу 2а (рис. 3.4). Если ф = 0, то а = 45° - максимальное значение, соответствующее максимальному напряжению сдвига на плоскости разрыва (разд. 2.3.2, уравнение (2)). Например, для диабаза, деформируемого при атмосферном давлении, константы С и µ будут составлять около 120 МПа и 1 соответственно.

Критерий Кулона не применим к области образования трещин растяжения (т_с < С), т. е. при очень низком всестороннем давлении. Аналогично он не применим и при очень высоком всестороннем давлении (рис. 3.5). Это обусловлено тем, что при высоком давлении материал становится более пластичным (рис. 3.2), и соответственно коэффициент внутреннего трения и наклон огибающей Мора уменьшаются. Таким образом, связь между т_с и ơ_с в этой области не описывается линейным уравнением критерия Кулона.

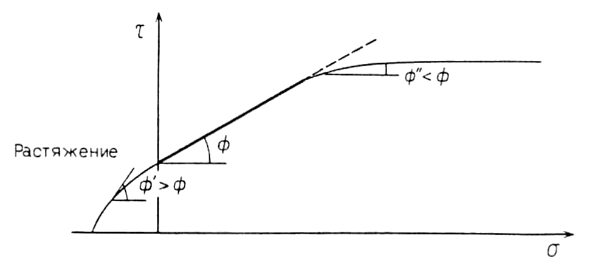
Рис. 3.5. Область применимости критерия Кулона на диаграмме Мора (жирная линия)

В естественных условиях повышение всестороннего давления с увеличением глубины, сопровождающееся ростом температуры (вследствие геотермического градиента), приводит к большей пластичности материала. Термический эффект проявляется также и в уменьшении наклона огибающей Мора.

Парциальное давление флюида и эффективное давление. Рассмотрим проницаемую пористую среду, насыщенную водой. На некоторой средней глубине z, равной, скажем, нескольким километрам, гидростатическое давление в жидкости равно 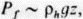, где плотность . Тогда нормальное напряжение, действующее на какую-либо площадку, уменьшается по сравнению с ơ_n из уравнения (1) (разд. 2.3.2) на величину Р_f, т.е.

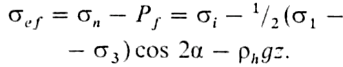
Величину 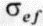называют эффективным давлением.

В этом примере мы считали, что межзерновое пространство проницаемой пористой среды сообщается с поверхностью, однако ниже определенной глубины это условие не выдерживается. Здесь такие процессы, как уплотнение, метаморфические реакции и частичное плавление, приводят к росту давления флюида (рис. 3.6). С увеличением глубины это давление стремится к давлению в твердой среде и временно может превысить его, если при этом происходит увеличение объема (разд. 3.2.5).

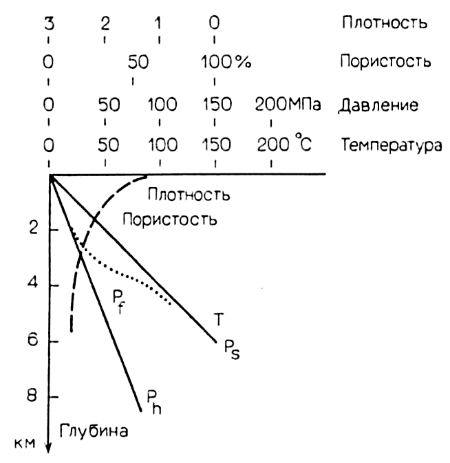
Рис. 3.6. Увеличение парциального давления флюидов вследствие уплотнения осадков и потери проницаемости (при произвольных Р. Т): Р, = 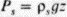- давление в твердой среде. p_hgz - гидростатическое давление в жидком столбе, р_s = 2,5рл.