Напряжения. Эллипсоид напряжений. Диаграмма Мора

На рис. 2.12, а иллюстрируется эксперимент, в котором к цилиндрическому образцу перпендикулярно его противоположным граням с площадью поверхности S приложены две противоположно направленные силы F. Каждая из сил создает давление Р = F/S, называемое нормальным напряжением 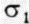. Приложенное напряжение в этом опыте является одноосным. В более сложном эксперименте тот же образец подвергается действию разных напряжений: 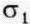- напряжение, приложенное перпендикулярно круговым сечениям, и 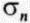- напряжение, нормальное к его боковой поверхности (рис. 2. 12, 6). В механике такой эксперимент называют трехосным испытанием. Можно считать, что цилиндрическая поверхность испытывает однородное нормальное напряжение 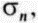а в круговых сечениях действуют избыточные напряжения 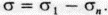Избыточное напряжение, вызывающее деформацию образца, называется дифференциальным или девиаторным.

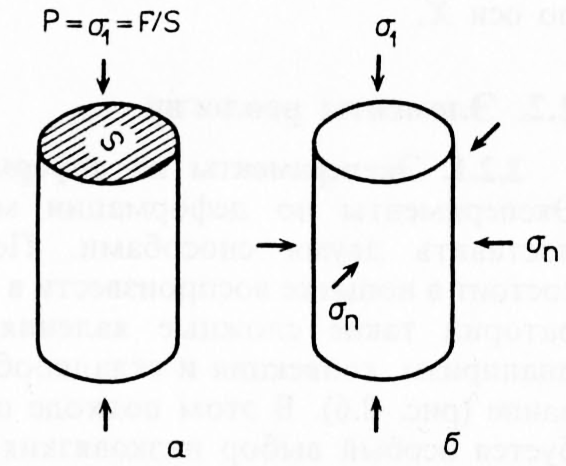
Рис. 2. 12. Деформация цилиндрического образца в одноосном (а) и трехосном (6) испытаниях

Еще более общую ситуацию можно вообразить, если взять образец в форме параллелепипеда (рис. 2. 13, а) и к трем взаимно перпендикулярным его граням приложить неравные напряжения 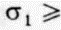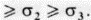. Изотропное давление, или среднее напряжение, определяется как 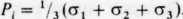Это можно считать гидростатической составляющей главных напряжений, и отсюда три главных дифференциальных напряжения выражаются соответственно в виде разностей . Вместо термина гидростатическое давление иногда применяют термины литостатическое или геостатическое давление, если речь идет о нагрузке, обусловленной массой вышележащих пород, или всестороннее давление - для условий эксперимента.

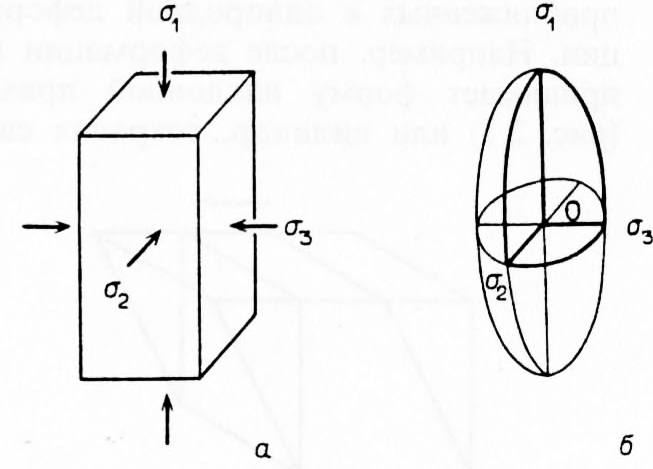
Рис. 2. 13. a-испытание образца под действием трех напряжений 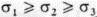, приложенных перпендикулярно граням; б - эллипсоид напряжений для испытания (а)

Напряженное состояние в точке О (рис. 2. 13, 6) алгебраически описывается с помощью шести независимых компонент тензора (см. приложение I), а его геометрическое представление дает эллипсоид напряжений, три полуоси которого равны соответственно трем главным (нормальным) напряжениям 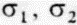и .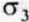

Литостатическое давление P_L на глубине z (недалеко от поверхности) создается вышележащей толщей пород и равно P_L = рgz, где р - плотность, g - ускорение силы тяжести. При отсутствии тектонических сил соответствующие горизонтальные напряжения удовлетворяют условию 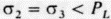. Лишь на глубине около 3 км, где все сдвиговые напряжения благодаря деформации исчезают, литостатическое давление Р_L становится изотропным: 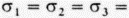= P_L. Именно с этих глубин начинается зона перехода к пластическому поведению пород (рис. 2. 14).

Рис. 2. 14

До сих пор мы говорили о напряжениях, соответствующих силам, приложенным перпендикулярно поверхности. Параллельно поверхности также могут быть приложены силы, создающие касательные или сдвиговые напряжения. Последние не являются сжимающими «давлениями», хотя и тоже определяются действующей на поверхность силой. Рассмотрим элемент поверхности SS' в точке X (рис. 2. 15), ориентированной некоторым образом относительно главного напряжения . Это напряжение можно разложить на две составляющие: 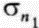-нормальное напряжение и 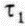-сдвиговое напряжение, действующее по касательной к поверхности SS' (рис. 2. 15).

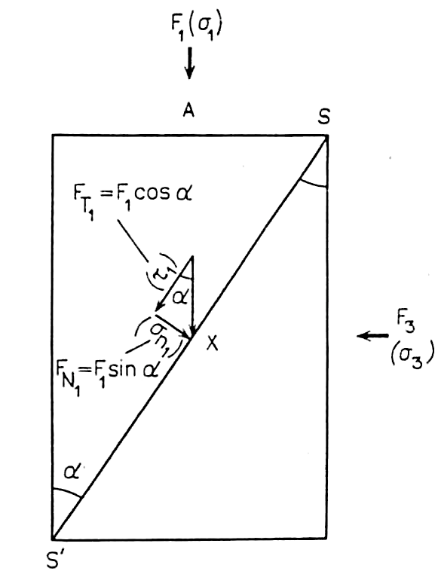
Рис. 2. 15. Разложение силы F₁ и соответствующих напряжений, действующих в точке X некоторой плоскости SS' (сечение, перпендикулярное оси )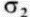

Если к образцу приложены разные главные напряжения (например, 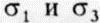на рис. 2. 15), то нормальная 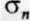и сдвиговая 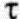компоненты напряжений в данной точке равны суммам

и

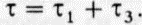
Диаграмма Мора. С помощью геометрического построения так называемой диаграммы Мора можно быстро определить сдвиговое 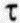и нормальное 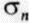напряжения на площадке заданной ориентации относительно главных направлений (осей) напряжений.

Пусть для простоты ơ₂ = ½ (ơ₁ + ơ ₃), т.е. ơ₂ = ơ_і где ơ_і - среднее давление. Тогда полное решение задачи получается в плоскости ơ₁ — ơ ₃. Обозначив через F₁ силу, действующую перпендикулярно поверхности А (рис. 2. 15), найдем ее компоненты в точке X на поверхности SS', расположенной под углом а к направлению F₁. Компонентами силы F₁ будут нормальная составляющая F_N1 и тангенциальная F_t1, отнесенные к единичной площадке, так что для нормального ơ_n1 и касательного t₁ напряжений получим

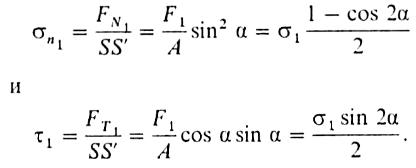
Аналогичное разложение силы F₃ дает ее вклад в нормальное ơ_n и касательное t напряжения на площадке в точке X. В результате мы приходим к следующим выражениям:

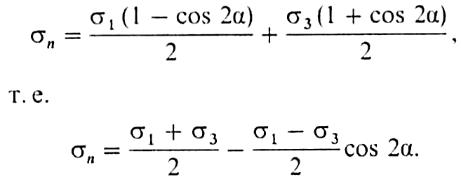
С учетом того, что ½ (ơ₁ + ơ₃) равно среднему давлению, находим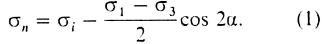

Аналогично получаем сдвиговое напряжение в виде

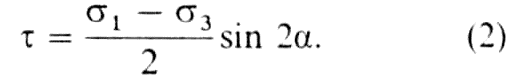
Представим теперь напряженное состояние в точке X поверхности SS' на координатной плоскости с касательным напряжением по ординате и нормальным напряжением по абсциссе (рис. 2. 16). Уравнения (1) и (2) задают окружность с центром в точке ½ (ơ₁ + ơ₃) и радиусом ½ (ơ₁ — ơ ₃). Ее называют кругом Мора, и на практике достаточно изобразить лишь половину этой окружности.

Главные напряжения ơ₁ и ơ₃ соответствуют точкам пересечения окружности с абсциссой, а напряжение ơ ₂ = ½ (ơ₁ + ơ ₃), согласно нашему первоначальному условию ơ₂ = ơ_і определяется центром круга. На плоскости, расположенной под углом а к направлению главного напряжения, действуют нормальное ơ_n и сдвиговое t напряжения, определяемые соответственно абсциссой и ординатой точки пересечения окружности с лучом, проведенным из ее центра под углом 2а к абсциссе. Таким образом, t = 0 при a = 0° и a = 90. т. е. на площадках, параллельных или перпендикулярных оси ơ₁ и достигает максимального значения 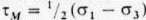при a = 45°. Этот анализ показывает характерное свойство площадок, перпендикулярных главным направлениям напряжений ơ₁ , ơ₂ и ơ ₃: на этих площадках действуют только нормальные напряжения.