Деформации и напряжения. Эллипсоид конечных деформаций

Определения. Под действием приложенных сил породы деформируются, и их смещение состоит из компонент, связанных с чистой деформацией, трансляцией (поступательным движением) и поворотом как твердого целого. Деформация в узком смысле - изменение формы тел. При трансляции все частицы породы имеют одинаковый вектор смещения, а при деформации этот вектор изменяется от точки к точке, т. е. в теле породы возникают градиенты смещений (рис. 2.1). Для математического описания деформаций применяются тензоры (приложение I).

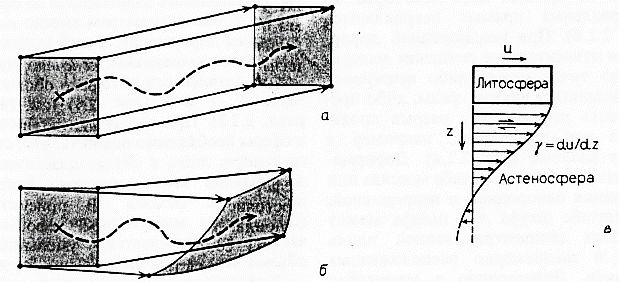
Рис. 2.1. Векторы смешения при трансляции (а) и деформации (б). В первом случае векторы смещения всех частиц равны, во втором не равны. Действительные траектории частиц при деформации (пунктир) не обязательно совпадают с их векторами смещения, которые определяются лишь их начальными и конечными положениями, «-иллюстрация движения верхней мантии вблизи океанического хребта. Жесткая литосфера целиком смещается на вектор 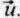. В деформируемой астеносфере имеется градиент смещения 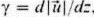, определяющий деформацию сдвига

Определение трансляций и вращений горных пород относительно географической системы координат является важной геологической задачей. Например, мы сталкиваемся с вопросом о смещении какого-либо тектонического покрова в горном поясе или об угле относительного поворота двух плит вокруг вертикальной оси (скажем, при вращении блока Корсика-Сардиния относительно Европы).

Ответ позволяют найти два подхода: в одном из них сравниваются начальное и конечное положения структуры при условии, что первое считается известным (в нашем примере это могут быть корневая зона покрова или положение блока по палеомагнитным данным); в другом анализируется интегральная деформация таких образований, как складки, зоны сдвига и другие структуры. Реализация этих идей рассматривается в гл. 7.

На рис. 2.6 и 2.7 показаны примеры соответственно неоднородной и однородной деформаций. В результате однородной деформации материальные точки среды, первоначально находившиеся на какой-либо прямой, также расположатся на некоторой прямой (рис. 2.2, а), в то время как после неоднородной деформации по крайней мере некоторые из материальных прямых искривляются (рис. 2.2, 6).

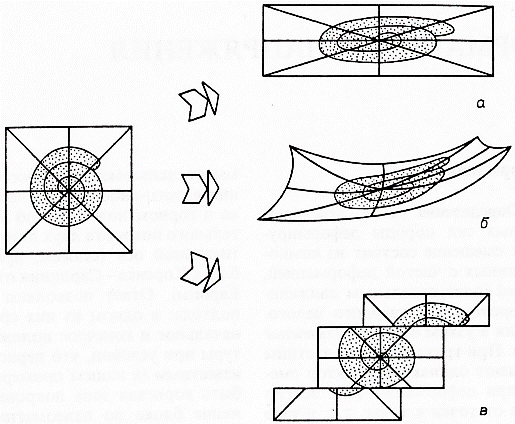
Рис. 2.2. а - непрерывная однородная деформация: прямые линии преобразуются в прямые; б - непрерывная неоднородная деформация; прямая линия, как правило, преобразуется в кривую; в - разрывная деформация

При неоднородной деформации относительное смещение материальных точек может либо непрерывно распределяться внутри среды, либо претерпевать разрыв. Этот разрыв проявляется как разрушение, например в случае разлома (рис. 2.2, в). Деформация, кажущаяся в масштабе массива или обнажения однородной и непрерывной, в масштабе штуфа или шлифа может оказаться сконцентрированной вдоль тесно и закономерно расположенных разрывов. Деформацию в масштабах массива или обнажения называют проникающей (рис. 2.3, а), а деформацию в масштабах образца или шлифа - непроникающей (рис. 2.3, 6).

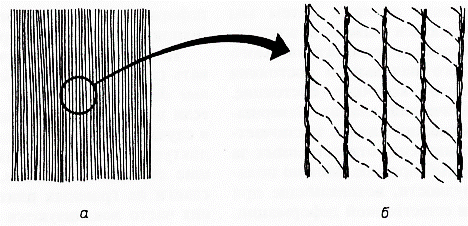
Рис. 2.3. Деформация, проникающая в масштабе обнажения (л) и непроникающая в масштабе образца (б)

Эллипсоид конечных деформаций. Допустим, что в породе содержатся маленькие сферические тельца, такие, как оолиты. После однородной деформации сферы превращаются в эллипсоиды. Из сравнения эллипсоидов со сферами по форме и размерам можно найти величины деформаций. Такой эллипсоид называется эллипсоидом конечных деформаций, главные оси которого обозначим через X, Y и Z (рис. 2.4) (см. также разд. 2.2.2). При сравнении эллипсоида и сферы необходимо помнить, что, строго говоря, лишь в случае пластической деформации явно допустимо условие постоянства объема. В присутствии флюида, как мы увидим, деформация часто сопровождается уменьшением объема вследствие вытеснения флюида.

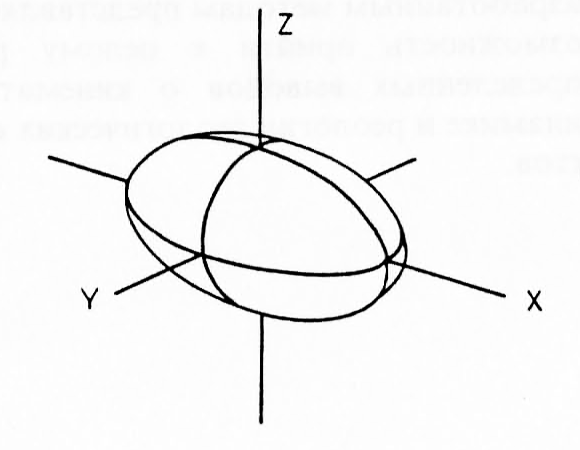
Рис. 2.4. Эллипсоид деформации с главными осями X ≥ Y ≥ Z

Характеристики однородной деформации устанавливаются с помощью различных индикаторов (жилы, гальки, окисленные или восстановленные пятна и т. п.) путем измерения длин главных осей эллипсоида деформаций в плоскостях XY, XZ и YZ. Если же деформация неоднородна, то рассматриваемый домен разбивается на части, в пределах которых деформацию с приемлемой точностью можно считать однородной (разд. 8.1). Поскольку индикаторов деформаций может быть много и их обработка требует специального анализа, процедура измерения деформаций весьма сложна. Более подробно этот вопрос рассматривается в приложении II.

Деформированное состояние. Деформацию наглядно описывает форма эллипсоида деформаций, который может быть, например, сплющенным или вытянутым по вертикали. Если ось Y эллипсоида остается неизменной при условии постоянного объема, то деформация является плоской. Различные виды деформированного состояния очень удобно представлять на диаграмме Флинна (рис. 2. 5), где параметр К определяет наклон прямой, проведенной через заданную точку на диаграмме и точку (1, 1):

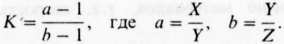
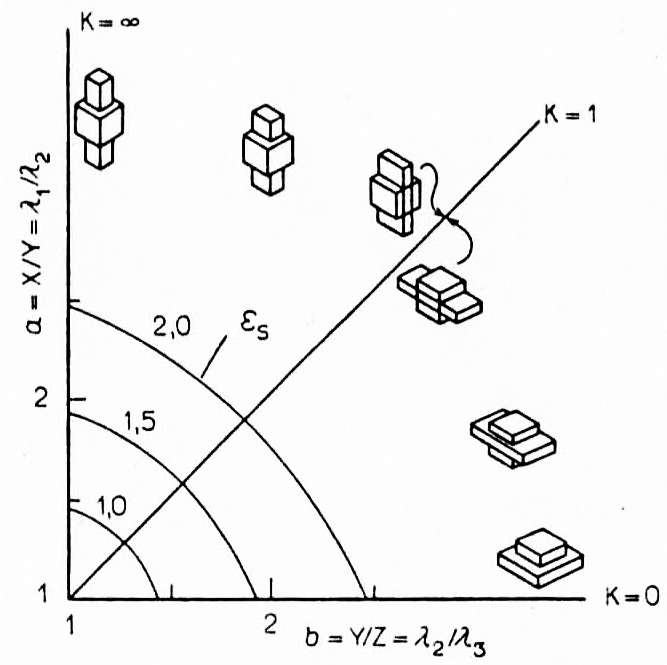
Рис 2. 5. Диаграмма Флинна, иллюстрирующая различные состояния конечной деформации и их связь с главными осями эллипсоида деформации. Фигурки иллюстрируют тип деформации в соответствующей области. Смысл параметров λ и Ɛ_s, объясняется в приложении

В зависимости от значения К на диаграмме выделяются различные области. Так. при К = 0 эллипсоид конечных деформаций становится эллипсоидом вращения, сплющенным, как блин, перпендикулярно оси Z. Если 0 < К < 1, то эллипсоид уже не фигура вращения, но по-прежнему сплющен. В области 1 < К < ∞ эллипсоид растянут и деформация носит характер обжатия. При К - ∞ эллипсоид вытянут, как сигара, по оси X.