Задачи, приводящие к понятию определенного интеграла

Задача 1. Найти массу тонкого прямолинейного стержня длины l с переменной линейной плотностью.

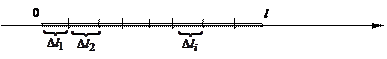Решение. Стержень тонкий – это значит, что поперечные размеры его столь малы по сравнению с длиной, что ими можно пренебречь. Предположим, что зависимость плотности от расстояния точки стержня до одного из его концов известна и может быть описана некоторой функцией. Составим математическую модель задачи следующим образом. Будем интерпретировать стержень с отрезком оси ОХ длины l , например с отрезком [0, l]. Тогда переменная плотность масс точек стержня есть функция переменной хÎ[0, l], обозначим ее r(х). Разобьем отрезок [0, l] на п произвольных частей и обозначим длины этих частичных отрезков Dl_i, i = 1,...,n.

Будем полагать, что п достаточно велико , а Dl_i достаточно малы. На каждом из этих отрезков разбиения возьмем произвольную точку x_i и в силу малости длины Dl_i можем предполагать, что величина плотности в пределах каждого частичного отрезка меняется незначительно и приближенно равна r(x_i). Тогда на каждом отрезке разбиения масса участка стержня приближенно равна m_i »r(x_i)Dl_i, а масса всего стержня 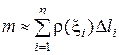и это равенство тем точнее, чем меньше Dl_i (т.е. чем больше п). Поэтому естественно считать искомую массу равной

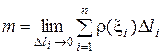
Задача 2. Найти площадь криволинейной трапеции, ограниченной кривой y = f(x), прямыми х = а и х = b и отрезком [a, b] оси ОХ.(рис .1).

Решение. Разобьем отрезок [a, b] на п произвольных частей точками х₁, х₂,..., х­_п, обозначим Dх_i длину частичного отрезке [x_i–1, x_i].

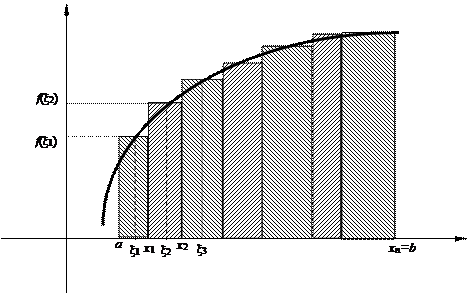
Построим прямоугольники с основаниями Dх_i и высотами f(x_i), где x_i – произвольная точка из отрезка [x_i–1, x_i]. Тогда сумма площадей этих прямоугольников приближенно равна площади заданной криволинейной трапеции

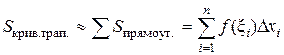
причем это приближенное равенство тем точнее, чем меньше Dх_i .Поэтому можно считать, что .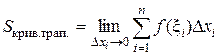

Если сравнить ответы в этих задачах, можно заметить , что в каждом из них содержатся выражения одинакового характера: предел суммы произведений значений заданной функции в точках отрезков разбиения на длины этих отрезков. Оказывается, существует множество других задач, совершенно различного содержания и из различных областей науки, которые приводят к пределам подобного рода. Поэтому естественно рассмотреть соответствующую абстрактную конструкцию .