МинимизацияФАЛ методом равносильных преобразований

Любая булева функция представима в СН(Д или К) формах. Более того, такое представление является первым шагом перехода от табличного задания функций к ее аналитическому выражению.

В дальнейшем будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получаются на основе принципа двойственности.

Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний).

Такие формы называют минимальными.

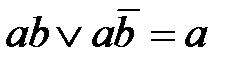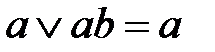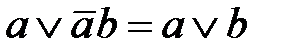Формула, представленная в ДНФ, упрощается многократным применением операции склеивания и операций поглощения и (дуальные тождества для конъюнктивной нормальной формы имеют вид:

).

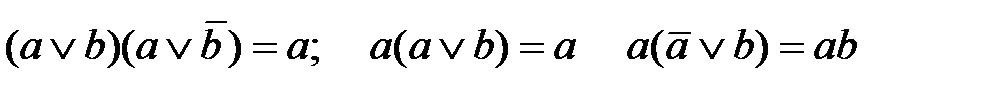Здесь под а и b можно понимать любую форму булевой алгебры.

В результате приходим к такому аналитическому выражению, когда дальнейшие преобразования оказываются невозможными, т.е. получаем тупиковую форму.

Среди тупиковых форм находится и минимальная ДНФ, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма – минимальная, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв.

Пример. Составить по таблице истинности СДНФ булевой функции 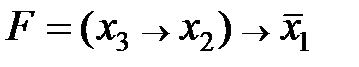и минимизировать ее, применяя законы склеивания.

Решение.

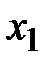
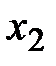
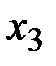
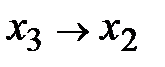
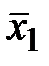
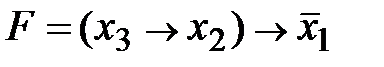
СДНФ будет иметь вид: .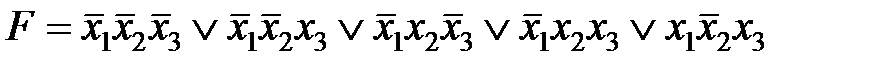

Минимизируем ее, применяя законы склеивания. Подчеркнем конъюнкции, которые можно склеить. Очевидно, что это можно сделать различными способами, например:

,

,

,

.

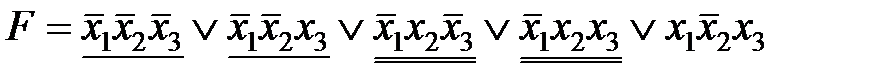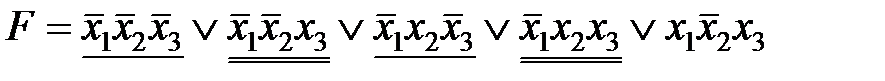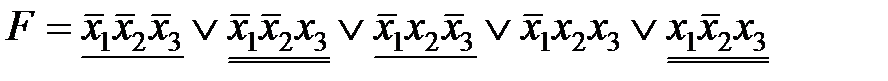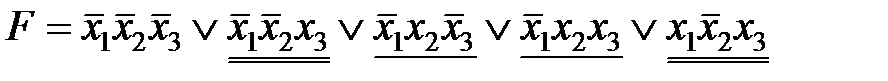Выберем один из возможных вариантов склеивания, например 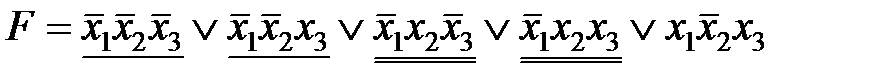и минимизируем ДНФ:

.

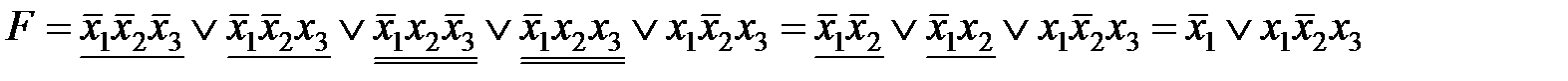Замечание.При минимизации ДНФ достаточно часто (но не всегда!) удается получить лучшие результаты, если «нарастить» данную ДНФ используя свойство идемпотентности дизъюнкции: .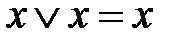

Например, в рассматриваемом примере пятую, последнюю конъюнкцию 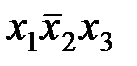можно было бы склеить со второй конъюнкцией 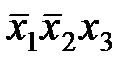. Добавив вторую конъюнкцию еще раз, мы не изменим саму булеву функцию, но получим в результате минимизации ДНФ более короткое ее представление:

.

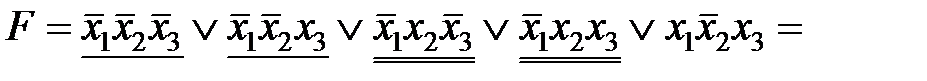
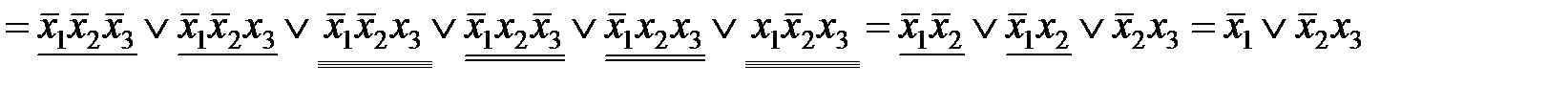Работа на таком уровне подобна блужданию. Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать графические и аналитические представления.

Пример. Составить СДНФ булевой функции, заданной вектором значений таблицы истинности w(F)=(10010010) и минимизировать ее, применяя законы склеивания.

Решение.Так как вектор значений заданной булевой функции имеет 8=2³ разрядов, следовательно, булевой функции соответствует следующая таблица истинности:

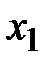
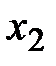
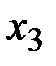
			F

СДНФ будет иметь вид: .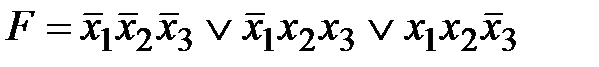

Минимизировать данную функцию, применяя законы склеивания, невозможно.