Метод неопределенных коэффициентов
Метод применим для минимизации функций алгебры логики от любого числа переменных.
Рассмотрим случай трех переменных. Булева функция в ДНФ может быть представлена в виде всевозможных конъюнктивных членов, которые могут входить в ДНФ:
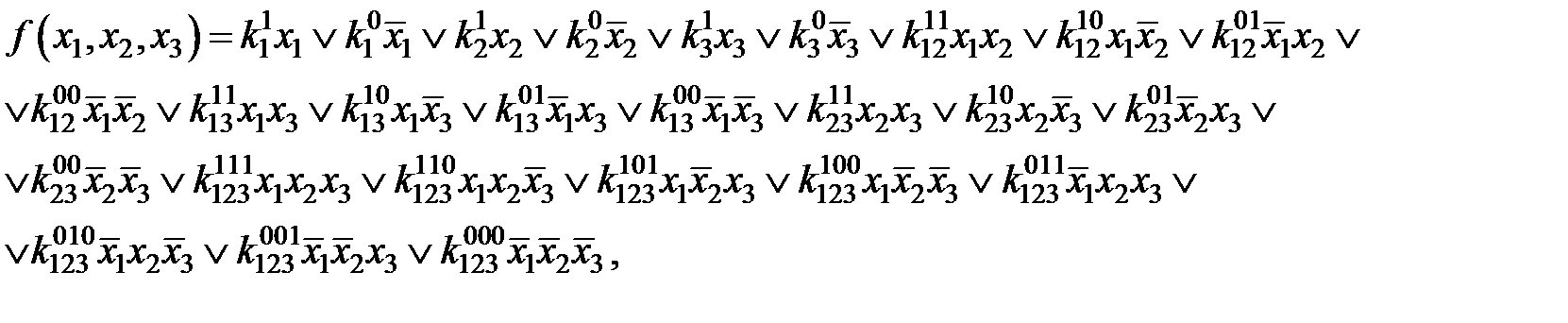
где kО{0,1}‑ коэффициенты. Метод заключается в подборе коэффициентов таким образом, чтобы получаемая ДНФ была минимальной.
Если теперь задать всевозможные значения переменных от 000 до 111, то получим 2n (23 =8) уравнений для определения коэффициентов k:
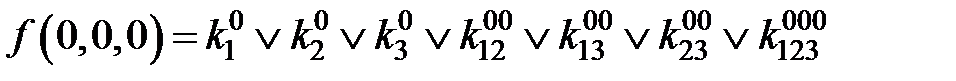 ;
;
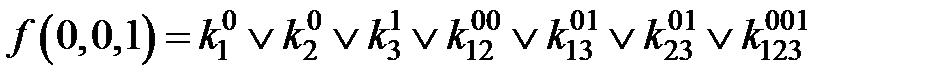 ;
;
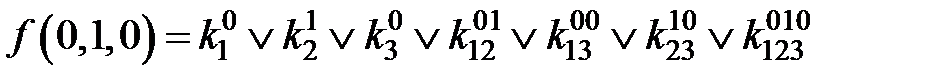 ;
;
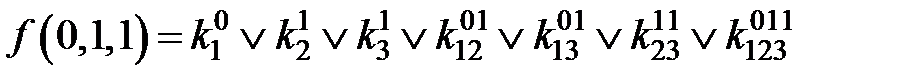 ;
;
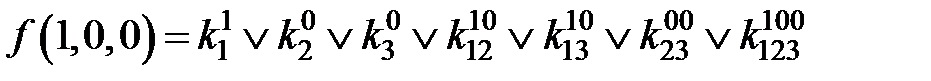 ;
;
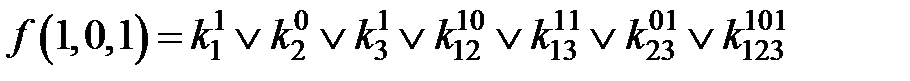 ;
;
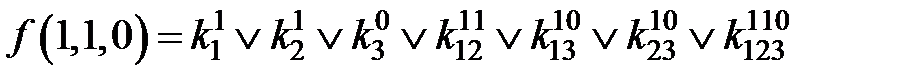 ;
;
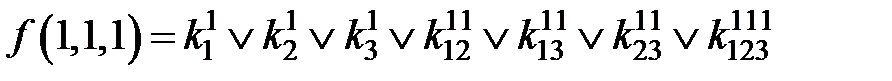 .
.
Рассматривая наборы, на которых функция принимает нулевое значение, определяют коэффициенты, которые равны 0, и вычеркивают их из уравнений, в правой части которых стоит 1. Из оставшихся коэффициентов в каждом уравнении к единице приравнивают по одному коэффициенту, определяющему конъюнкцию наименьшего ранга. Остальные коэффициенты приравнивают к 0. Итак, единичные коэффициенты k определяют соответствующую минимальную форму.
Алгоритм определения коэффициентов:
1. Исходное уравнение разбить на систему уравнений, равных числу строк в таблице истинности.
2. Напротив каждого выражения поставить соответствующее значение функции.
3. Выбрать строку, в которой значение функцииf=0и приравнять все kiк нулю.
4. Просмотреть строки, где функция имеет единичное значение, и вычеркнуть все коэффициенты, встречающиеся в нулевых строках.
5. Проанализировать оставшиеся коэффициенты в единичных строках.
6. Используя правило, что дизъюнкция равна 1 если хотя бы один из ki=1, выбрать min-термы минимального ранга. Причем отдавать предпочтение коэффициентам, встречающимся в нескольких уравнениях одновременно.
7. Записать исходный вид функции.
Пример. Минимизировать заданную функцию
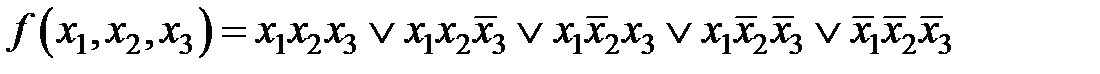 ,если известны значения:
,если известны значения: 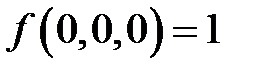 ;
; 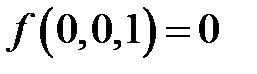 ;
; 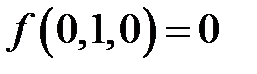 ;
; 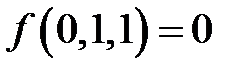 ;
; 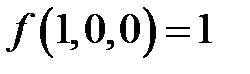 ;
; 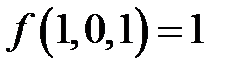 ;
; 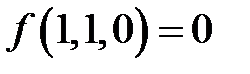 ;
; 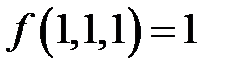 .
.
Решение.
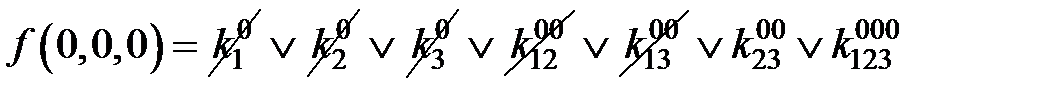 =1;
=1;
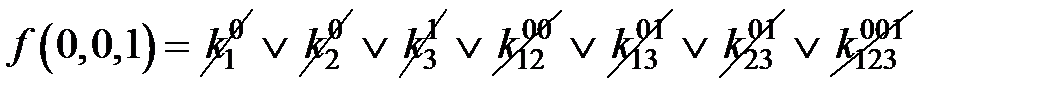 =0;
=0;
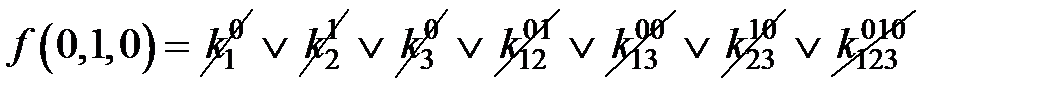 =0;
=0;
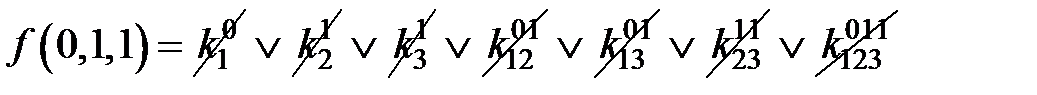 =0;
=0;
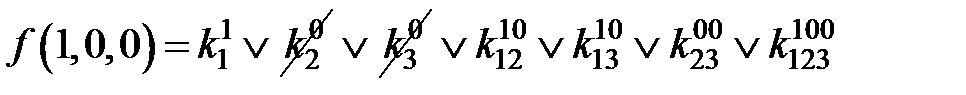 =1;
=1;
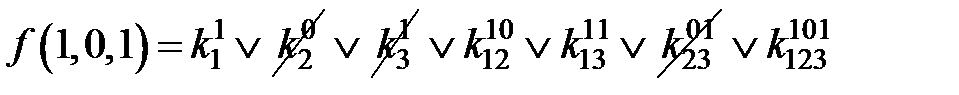 =1;
=1;
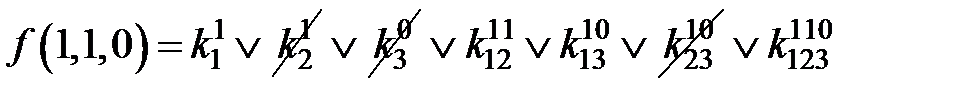 =1;
=1;
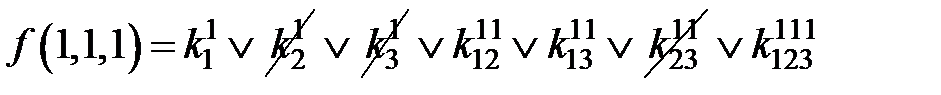 =1.
=1.
После вычеркивания нулевых коэффициентов получим:
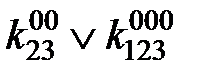 =1;
=1;
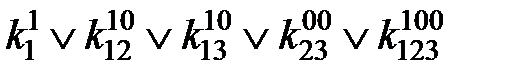 =1;
=1;
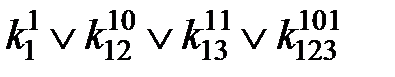 =1;
=1;
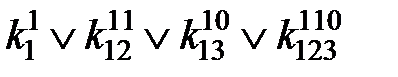 =1;
=1;
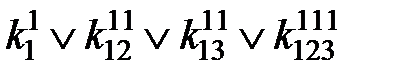 =1.
=1.
Приравняем к единице коэффициент 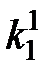 , соответствующий конъюнкции наименьшего ранга и обращающий четыре последних уравнения в 1, а в первом уравнении целесообразно приравнять к 1 коэффициент
, соответствующий конъюнкции наименьшего ранга и обращающий четыре последних уравнения в 1, а в первом уравнении целесообразно приравнять к 1 коэффициент 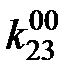 . Остальные коэффициенты приравнивают к 0.
. Остальные коэффициенты приравнивают к 0.
Ответ: вид минимизированной функции 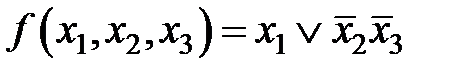 .
.
Следует отметить, что метод неопределенных коэффициентов эффективен, когда число переменных невелико и не превышает 5-6.
Многомерный куб
Рассмотрим графическое представление функции в виде многомерного куба. Каждой вершине n-мерного куба можно поставить в соответствие конституенту единицы.

Подмножество отмеченных вершин является отображением на n-мерном кубе булевой функции от n переменных в СДНФ.
Для отображения функции от n переменных, представленной в любой ДНФ, необходимо установить соответствие между ее min-термами и элементами n-мерного куба.
min-терм (n-1)-го ранга 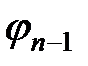 можно рассматривать как результат склеивания двух min-термов n-го ранга, т.е.
можно рассматривать как результат склеивания двух min-термов n-го ранга, т.е. 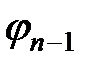 =
= 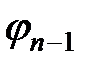
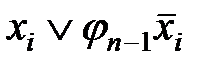
На n-мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координат хi, соединяющих эти вершины ребром (говорят, что ребро покрывает инцидентные ему вершины).
Таким образом, min-термам (n-1)-го порядка соответствуют ребра n-мерного куба.
Аналогично устанавливается соответствие min-термов (n-2)-го порядка граням n-мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).
Элементы n-мерного куба, характеризующиеся S измерениями, называются S-кубами.
Так вершины являются 0-кубами, ребра 1-кубами, грани 2-кубами и т.д.
Обобщая, можно сказать, что min-терм (n-S) ранга в ДНФ для функции n переменных отображается S-кубом, причем каждый S-куб покрывает все те кубы низшей размерности, которые связаны только с его вершинами.
Пример. На рис 3.1. дано отображение 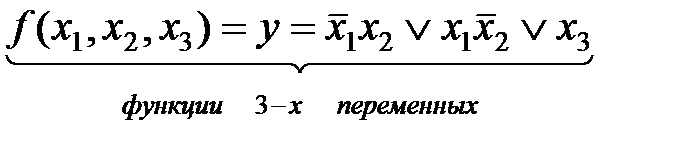
 рис. 3.1
рис. 3.1
Здесь min-термы 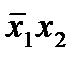 и
и 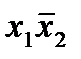 соответствуют 1-кубам (S=3-2=1), а min-терм х3 отображается 2-кубам (S=3-1=2).
соответствуют 1-кубам (S=3-2=1), а min-терм х3 отображается 2-кубам (S=3-1=2).
Итак, любая ДНФ отображается на n-мерном кубе совокупностью S-кубов, которые покрывают все вершины, соответствующие конституентам единицам (0-куба).
Конституенты. Для переменных х1, х2,…хn выражение 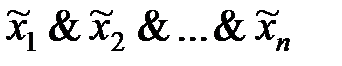 называют конституентой единицы, а
называют конституентой единицы, а 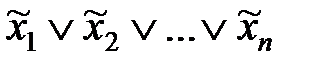 — конституентой нуля (
— конституентой нуля ( 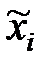 означает либо
означает либо 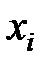 , либо
, либо 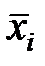 ).
).
Даннаяконституента единицы (нуля) обращается в единицу (нуль) только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице (нулю), а их отрицания – нулю (единице).
Пример:конституенте единице 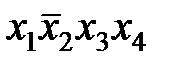 соответствует набор (1011), а конституенте нуля
соответствует набор (1011), а конституенте нуля 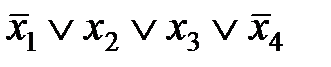 – набор (1001).
– набор (1001).
Так как СД(К)НФ является дизъюнкцией (конъюнкцией) конституент единицы (нуля), то можно утверждать, что представляемая ею булева функция f(x1,x2,…,xn) обращается в единицу (нуль) только при наборах значений переменных x1,x2,…,xn, соответствующих этим копституантам. На остальных наборах эта функция обращается в 0 (единицу).Справедливо и обратное утверждение, на котором основан способ представления в виде формулы любой булевой функции, заданной таблицей (см. Лекцию 2).
Справедливо и обратное утверждение: если некоторая совокупность S-кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим S-кубам min-термов является выражением данной функции в ДНФ.
Говорят, что такая совокупность S-кубов (или соответствующих им min-термов) образует покрытие функции. Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число S-кубов которого было бы поменьше, а их размерность S–побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием.
Пример.для функции 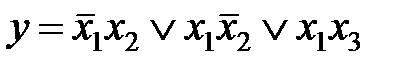 покрытие соответствует неминимальной форме:рис a)
покрытие соответствует неминимальной форме:рис a) 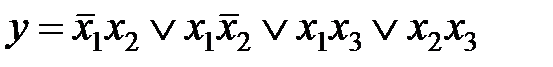 ,
,
а покрытия на рис б) 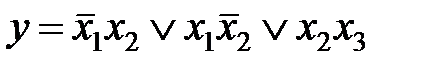 ,
,
рис в) 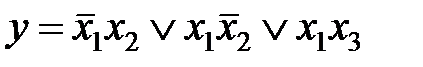 минимальные.
минимальные.



Рис. 3.2. Покрытие функции 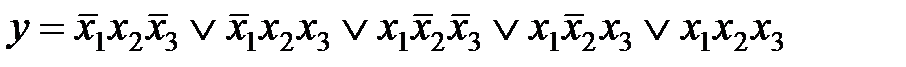 :
:
а) неминимальное; б), в) минимальное.
Отображение функции на n-мерном наглядно и просто при n£3.
Карты Карно
В другом методе графического отображения булевых функций используют карты Карно – специально организованные таблицы соответствия.
Столбцы и строки таблицы соответствуют всевозможным наборам значений не более 2-х переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством.

Рис. 3.3. Карты Карно для 2-х и 3-х переменных.

Рис. 3.4. Карты Карно для 4-х переменных.
Как и в обычных таблицах соответствия клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписываются, им соответствуют пустые клетки).
Пример.На рис. 3.5. показана упрощенная карта Карно для функции, 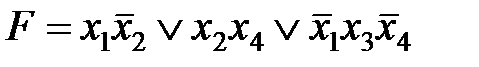 Для упрощения строки и столбцы, соответствующие значениям “1” для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.
Для упрощения строки и столбцы, соответствующие значениям “1” для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.

Рис. 3.5. а) отображение функции четырех переменных;
б) отображение ее минимального покрытия.
Между отображениями функции на n-мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно S-кубу соответствует совокупность 2-х соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике. Поэтому все положения, изложенные ранее, справедливы и для карт Карно. Так на рис. 3.5. б) показано покрытие единиц карты, соответствующее минимальной дизъюнктивной форме 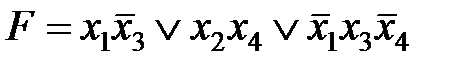 , рассматриваемой функции.
, рассматриваемой функции.
Считывание min-термов с карты Карно осуществляется по простому правилу. Клетки, образующие S-куб, дают min-терм (n-S)-го ранга, в который входят те (n-S)-переменные, которые сохраняют одинаковые значения на этом S-кубе, причем значениям “1” соответствуют сами переменные, а значениям “0” их отрицание.
Переменные, которые не сохраняют свои значения на S-кубе, в min-терме отсутствуют. Различные способы считывания приводят к различным представлениям функции в ДНФ.

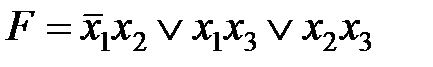
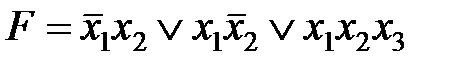

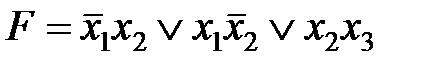
Использование карт Карно требует более простых построений по сравнению с отображением на n-мерном кубе, особенно в случае 4-х переменных.
Для отображения функций 5-ти переменных используют две карты Карно на 4-ре переменные, а для функции 6-ти переменных – четыре таких карты.
При дальнейшем увеличении числа переменных карты Карно становятся практически непригодны.
Метод Квайна
Метод Карно позволяет минимизировать логические функции с относительно малым числом переменных. Кроме того метод является визуальным и сложным для алгоритмизации.
Этот метод применим к функции, записанной в СДНФ. Решение задачи минимизации булевой функции методом Квайна базируется на понятиях импликант. В отношении импликант булевой функции также как и в отношении кубов, соответствующих им, существует отношение покрытия. Принято считать,что импликанта покрывает некоторую существенную вершину или в общем случае некоторый куб, если значение импликанты на наборе аргументов, представляющем данную существенную вершину, равно или в общем случае значение импликанты равно для всех существенных вершин, покрываемых кубом.
Пример:импликанта x1x2 покрывает существенные вершины (110,111) и в свою очередь покрывает куб «11*».
Определение. Множество импликант булевой функции образует полную систему импликант (является покрытием булевой функции), если любая существенная вершина булевой функции покрывается хотя бы одной импликантой этого множества.
Если считать,что в полную систему импликант включаются импликанты только в виде конъюнкций и не включаются импликанты в виде дизъюнкций, то полной системе импликант можно поставить в соответствие некоторое множество кубов, образующих покрытие булевой функции.
Определение. Система простых импликант называется приведенной, если она является полной и никакая ее собственная часть уже не образует полную систему импликант.
Минимизация функции проводится поэтапно.
1 этап. Нахождение первичных импликант. Все конъюнкции СДНФ данной функции (0-кубы) сравнивают между собой попарно, применяя закон склеивания. Удобно члены функции занумеровать и расположить в таблице (импликатной матрице).
| Члены функции f(x1, x2, x3) | Результаты первого склеивания | Результаты второго склеивания | … |
| 1. | 1. | 1. | |
| 2. | 2. | 2. | |
| … | … | … |
1-й член последовательно сравнивается со всеми остальными. Результаты склеивания записываются во 2-й столбец, указывая в скобках номера склеенных членов, а склеенные члены 1-го столбца отметить звездочкой «*». Ранг полученных конъюнкций на единицу ниже (1-кубы), т.е. они содержат на один знак меньше. Эти конъюнкции нумеруются, затем операцию повторяют, записывая результат в 3-й столбец и т.д. Заканчивают эту процедуру, когда вновь полученные конъюнкции уже не склеиваются между собой. Если в результате склеивания получаются одинаковые импликанты, то оставляют только одну из них. Все неотмеченные знаком «*» конъюнкции являются первичными (простыми импликантами). Все отмеченные конъюнкции будут поглощены простыми импликантами (закон поглощения). Все простые импликанты в таблице обводятся рамками. Дизъюнкция всех простых импликант дает сокращенную ДНФ данной функции. Далее необходимо перейти к тупиковой ДНФ. Это уже 2-й этап.
2 этап. Расстановка меток. Составляется таблица, число строк которой равно числу найденных простых импликант, а число столбцов – числу членов СДНФ данной функции. В 1-й столбец записываются первичные импликанты, в 1-ю строку все 0-кубы функции. Если 0-куб функции покрывается простой импликантой, то на пересечении их строки и столбца ставится метка «v». У простых импликант 3-го порядка метки удобно проставить по номерам склеенных членов 1-го столбца, приписанным у импликант рядом (в скобках), а у первичных импликант2-го порядка по номерам членов 1-го столбца. Число меток в строке зависит от числа исключенных букв в импликанте. Для k исключенных букв число меток будет 2k .
3 этап. Нахождение существенны химпликант. Если в каком-либо столбце составленной таблицы меток имеется только одна метка, то первичная импликанта, стоящая в соответствующей строке, является существенной. Она не может быть исключена из минимальной формы функции, т.к. без нее не может быть получено покрытие всего множества импликант данной функции. Из таблицы меток исключаются строки и столбцы, на пересечении которых стоит эта единственная метка.
4 этап. Вычеркивание лишних столбцов. Если в таблице после 3-го этапа два одинаковых столбца (в которых метки стоят в одинаковых строках), то один из них вычеркивается, т.к. покрытие оставшегося столбца будет осуществлять покрытие выброшенной исходной импликанты.
5 этап. Вычеркивание лишних строк. Если в таблице после 4-го этапа появились строки в которых нет ни одной метки, то их вычеркивают, т.е. первичные импликанты, соответствующие им, исключаются из минимальной формы функции, т.к. они не покрываются оставшихся исходных импликант.
6 этап. Выбор минимального покрытия. Исследуем таблицу, полученную после всех предыдущих этапов (см. 3-й этап). Выбирается такая совокупность первичных импликант, которая бы имела метки во всех столбцах. Предпочтение отдается варианту покрытия с минимальным числом букв в первичных импликантах, образующих покрытие.
Замечания: 1. В методе Квайна есть одно существенное неудобство – необходимость полного попарного сравнения на этапе нахождения первичныхимпликант. С ростом числа аргументов функции и определяющих ее членов СДНФ растет число этих сравнений. Этот рост характеризуется фактариальной функцией. Поэтому применение метода Квайна становится затруднительным.
2. По методу Квайна получаются тупиковые формы. Их может быть несколько. Среди них и надо искать минимальные формы.
Пример.Минимизировать функцию 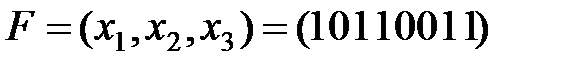 .
.
Решение. Поместим все 0- кубы функцииFв первый столбец таблицы и занумеруем их. Применим закон склеивания, результат запишем во второй столбец таблицы, снова занумеруем их, склеенные члены первого столбца отметим «*», и перейдем ко второму столбцу.
0-кубы 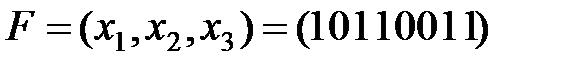 . .
| Результаты первой склейки | Результаты второй склейки | |
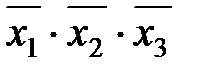 * *
| 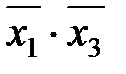 (1,2) (1,2)
| 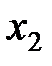 (2,5) (2,5)
| |
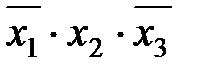 * *
| 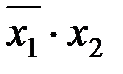 * (2,3) * (2,3)
| 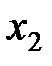 (3,4) (3,4)
| |
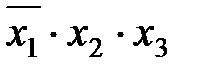 * *
| 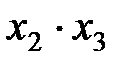 * (2,4) * (2,4)
| ||
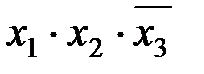 * *
| 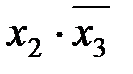 * (3,5) * (3,5)
| ||
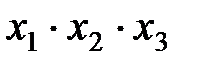 * *
| 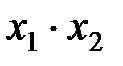 * (4,5) * (4,5)
|
Не склеившиеся простые импликаты обводим рамочкой. Дизъюнкция их дает сокращенную ДНФ. В данном примере первый этап оказался окончательным.
МДНФ: 
В общем случае надо перейти от сокращенной формы к тупиковой, а затем к минимальной.
Пример.Минимизировать функцию 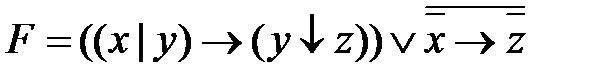
Решение. Воспользуемся упрощенным алгоритмом метода Квайна.
1. Получить СДНФ.
2. Получить сокращенную ДНФ (СкДНФ), используя следующие равносильности:
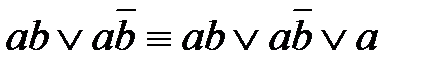 – неполное склеивание;
– неполное склеивание;
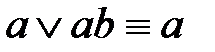 – поглощение.
– поглощение.
3. Построить импликантную матрицу, с помощью которой получить МДНФ.
1. 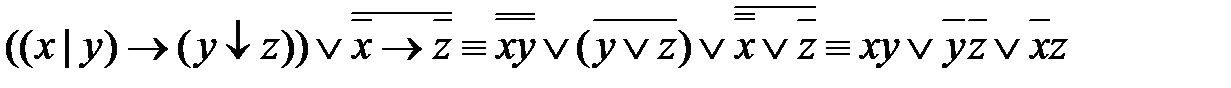 - ДНФ
- ДНФ
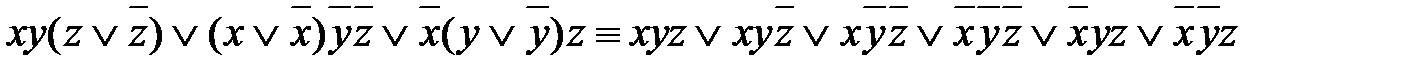 - СДНФ
- СДНФ
1 2 3 4 5 6
2. Применяя операции склеивания, получаем СкДНФ.
| 1-2: | 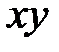
|
| 1-5: | 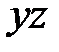
|
| 2-3: | 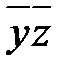
|
| 3-4: | 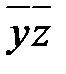
|
| 4-6: | 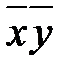
|
| 5-6: | 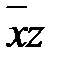
|
3. Составляем импликантную матрицу
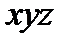
| 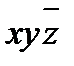
| 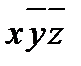
| 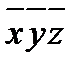
| 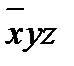
| 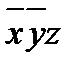
| |
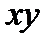
| + | + | ||||
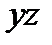
| + | + | ||||
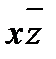
| + | + | ||||
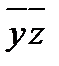
| + | + | ||||
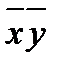
| + | + | ||||
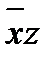
| + | + |
Выбираем импликанты, которые поглощают все конституенты единицы.
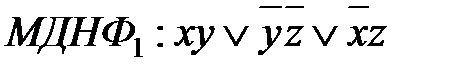
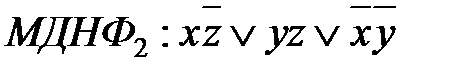
Дата добавления: 2021-10-28; просмотров: 709;











