Работа и мощность, энергия

I. Работа

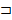тело под действием силы 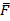, двигаясь по некоторой траектории, проходить путь S. Действие силы 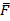на пути S характеризуется работой.

Работой называется скалярная физическая величина, равная произведению проекции силы на направления перемещения F_s и пути S, проходимого точкой приложения силы:

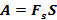
Это выражение справедливо при неизменной проекции силы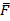

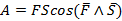
Вычисление работы

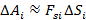
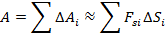Вообще говоря

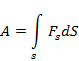
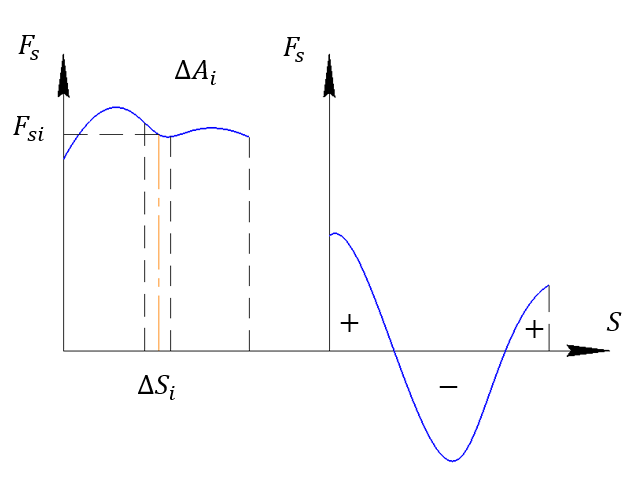
Т.о. работу, совершенная силой на пути S, можно вычислить, как площадь под графиком F_s(S)

Работа упругой силы

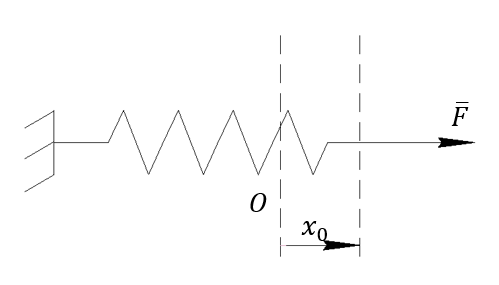
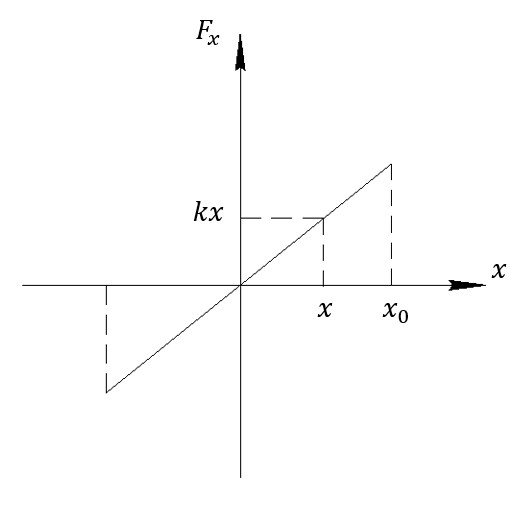
Растяжение будем производить медленно, чтобы приложенная сила была равна упругой

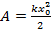– работа приложенной силы, равная площади треугольника под графиком

При этом работа упругой силы всегда равна 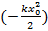, т.к. упругая сила всегда противоположна по направлению перемещению точки приложения силы.

II. Мощность

Для характеристики механизмов необходимо определить время совершения работы – мощность – величина, показывающая, какую работу совершает данный механизм в единицу времени.

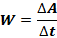
В общем случае, когда за одинаковые промежутки времени совершает различная работа

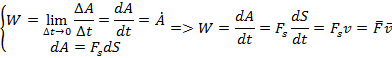
III. Энергия

Как показывает опыт, тела имеют свойство совершать работу над другими телами

Энергия – скалярная физическая величина, характеризующая способность тела или системы тел совершать работу.

Энергия тела может быть обусловлена:

-движением тела;

-нахождением тела в потенциальном поле сил.

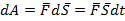Тело 1 совершает работу над телом 2 за счет запаса энергии, которым оно обладало вследствие своего движения 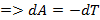Тогда

1) Кинетическая энергия

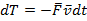
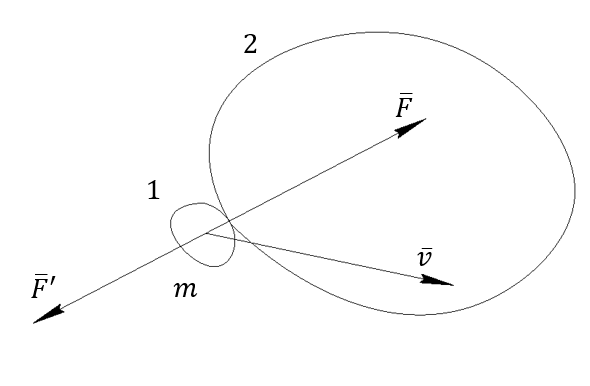
По третьему закону Ньютона: 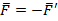, вследствие чего тело 1 получает приращение скорости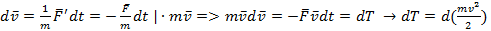

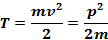
Работа, совершаемая над телом, равна приращению его кинетической энергии

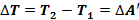
1) Потенциальная энергия

Рассмотрим тело в потенциальном поле сил. Сопоставим каждой точке поля, характеризуемой радиус-вектором 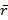определенное значение функции 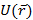, причем значение функции в точке 1:

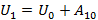
, где U₀ – потенциальная энергия точки, принятой за начало отсчета; А₁₀ – работа по перемещению из «1» в «0».

Аналогично для точки «2»: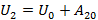

Тогда

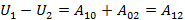
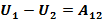
Т.о. с помощью функции 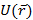можно определить работу, совершаемую над телом силами поля на любом пути. Она оказывается равной убыли функции 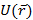=. Именно это дает основание назвать функцию 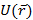одним из видов механической энергии – потенциальной энергией.

Т.к. U₀ – произвольное, то значение U определяется с точностью до некоторой постоянной. При этом для различных потенциальных полей U₀ уславливаются принимать по-разному:

-вблизи поверхности Земли ;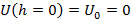

-на орбите .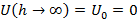

Примеры

Поле силы тяжести вблизи поверхности Земли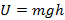

Поле упругой силы (пружина в пределах зоны упругости)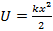

Сумма кинетической и потенциальной энергии тела называют полной механической энергией тела.

Теоретический минимум:

1) Работа

2) Вычисление работы

3) Работа силы тяжести и упругой силы

4) Мощность, формулы вычисления механической мощности

5) Энергия. Разновидности

6) Кинетическая энергия

7) Потенциальная энергия

8) Полная механическая энергия

<== предыдущая лекция	\|	следующая лекция ==>
Принцип суперпозиции	\|	Метод и методология.

Дата добавления: 2021-10-28; просмотров: 243;