ТЕОРЕМА О СОВМЕСТИМОСТИ (СЛАУ)

В общем виде система линейных алгебраических уравнений с n неизвестными x₁, x₂, ..., x_n записывается так:

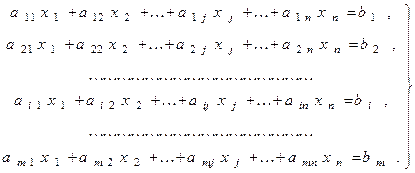(1)

Кратко СЛАУ (1) может быть записана так:

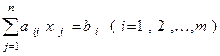(2)

или

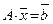
где

A= 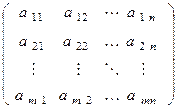, 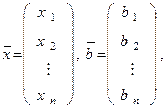(3)

ОПРЕДЕЛЕНИЕ 1. Если присоединить к матрице А столбец свободных членов, то получится матрица 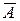, которая называется расширенной матрицей СЛАУ (1):

A= 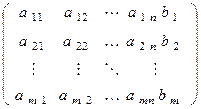(4)

Из определения матрицы A СЛАУ (1) и расширенной матрицы 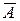ясно, что их ранг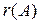и и 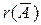либо равны между собой, либо ранг 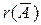на единицу больше, чем 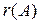. Вопрос о совместности СЛАУ (1) решается с помощью теоремы Кронекера-Капелли.

ТЕОРЕМА 1. СЛАУ (1) совместна тогда и только тогда, когда ранг расширенной матрицы 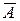равен рангу матрицы A, то есть когда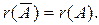

ПРИМЕР. Исследовать на совместимость следующую СЛАУ:

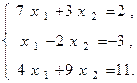
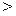Составим матрицу данной системы и вычислим ее ранг:

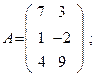
поскольку 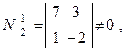то .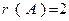

Далее , составим расширенную матрицу системы

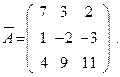
Так как 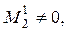а окаймляющий его минор

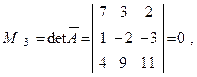то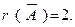

Итак, 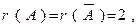то есть данная система совместна.

СЛЕДСТВИЕ 1. Если СЛАУ (1) совместна и ранг матрицы A системы (1) равен числу неизвестных п, то система имеет единственное решение.

СЛЕДСТВИЕ 2.Если система (1) совместна и ранг матрицы 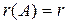меньше числа неизвестных n, то система имеет бесчисленное множество решений.

ТЕОРЕМА 2.Система n линейных уравнений с n неизвестными, определитель которой отличен от нуля всегда совместна и имеет единственное решение, вычисляемое по формулам

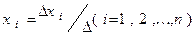
где

,

.

.

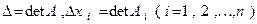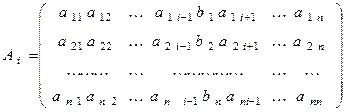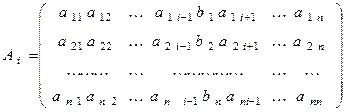4. РЕШЕНИЕ НЕОДНОРОДНОЙ СЛАУ ИЗ m УРАВНЕНИЙ

С n НЕИЗВЕСТНЫМИ

Пусть дана система m линейных алгебраических уравнений с n неизвестными (1). Пусть ranqA= ranq 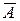, то есть система совместна. Не ограничиваясь общностью, будем считать, что базисный минор располагается в первых 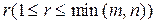строках и столбцах матрицы A. Отбросив последние m-r уравнений системы (1), запишем укороченную систему

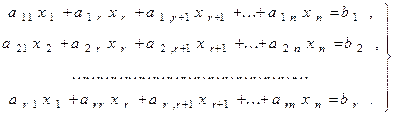(2)

которая эквивалентна исходной.

Назовем неизвестные x₁ ,x₂ , ..., x_r базисными, а x_r+1 , ..., x_n- свободными. Перенесем слагаемыe, содержащие свободные неизвестные, в правую часть уравнения (2). В результате, получим систему линейных алгебраических уравнений относительно базисных неизвестных

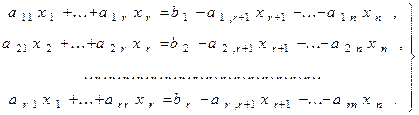(3)

которая для каждого набора значений свободных неизвестных x_r+1= c₁, x_r+2= c₂, ..., x_n=c_n-r. имеет единственное решение: x₁= f₁,(c₁, c₂ , ..., c_n-r), x₂= f₂,(c₁, c₂ , ..., c_{n-r), ...,} x_r= f_r,(c₁, c₂ , ..., c_{n-r). Решение системы (3) можно} определить либо по методу Крамера, либо методом Гаусса.

Общее решение СЛАУ можно записать в виде матрицы-столбца следующим образом:

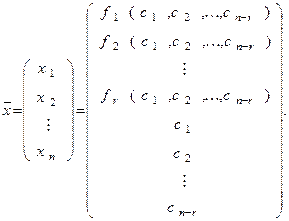(4)